在實分析或數學分析中,達布積分([Darboux integral] 錯誤:{{Lang-xx}}:參數 |links= 和 |link= 衝突(幫助))是一種定義一個函數的積分的方法,它是通過達布和構造的。達布積分和黎曼積分是等價的,也就是說,一個實值函數是達布可積的若且唯若它是黎曼可積的,並且積分的值相等。達布積分的定義比黎曼積分簡單,並且更具操作性。達布積分的名字來自於數學家讓·加斯東·達布。
一個閉區間![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 的一個分割是指在此區間中取一個有限的點列
的一個分割是指在此區間中取一個有限的點列 。每個閉區間
。每個閉區間![{\displaystyle [x_{i},x_{i+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7138606cdb8eb7dddaba59b5aefe1ade6bc05a1b) 叫做一個子區間。定義
叫做一個子區間。定義 為這些子區間長度的最大值:
為這些子區間長度的最大值: ,其中
,其中 。
。
再定義取樣分割。一個閉區間![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 的一個取樣分割是指在進行分割
的一個取樣分割是指在進行分割 後,於每一個子區間中
後,於每一個子區間中![{\displaystyle [x_{i},x_{i+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7138606cdb8eb7dddaba59b5aefe1ade6bc05a1b) 取出一點
取出一點  。
。 的定義同上。
的定義同上。
精細化分割:設 以及
以及 構成了閉區間
構成了閉區間![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 的一個取樣分割,
的一個取樣分割, 和
和 是另一個分割。如果對於任意
是另一個分割。如果對於任意 ,都存在
,都存在 使得
使得 ,並存在
,並存在 使得
使得 ,那麼就把分割:
,那麼就把分割: 、
、 稱作分割
稱作分割 、
、 的一個精細化分割。簡單來說,就是說後一個分割是在前一個分割的基礎上添加一些分點和標記。
的一個精細化分割。簡單來說,就是說後一個分割是在前一個分割的基礎上添加一些分點和標記。
於是我們可以在此區間的所有取樣分割中定義一個偏序關係,稱作「精細」。如果一個分割是另外一個分割的精細化分割,就說前者比後者更「精細」。
設![{\displaystyle f:[a,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc0d2d0b70573525d149ab82948308455d1853d0) 為一個有界函數,又設
為一個有界函數,又設

是閉區間![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 的一個分割。令:
的一個分割。令:
![{\displaystyle M_{i}=\sup _{x\in [x_{i-1},x_{i}]}f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25c5ca1d93d5d8b747695d7c0b093f6c5332f86b)
![{\displaystyle m_{i}=\inf _{x\in [x_{i-1},x_{i}]}f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a17031ef039871a0991cf7e24a13b658f8c50b02)
 下(綠色)和上(淡紫色)達布和
下(綠色)和上(淡紫色)達布和
 在分割
在分割 下的上達布和定義為:
下的上達布和定義為:

同樣的有下達布和的定義:

 的上達布積分指的是所有上達布和的下確界:
的上達布積分指的是所有上達布和的下確界:
 是閉區間
是閉區間![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 的一個分割
的一個分割
同樣的 的下達布積分指的是所有下達布和的上確界:
的下達布積分指的是所有下達布和的上確界:
 是閉區間
是閉區間![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 的一個分割
的一個分割
如果 那麼
那麼 就稱作達布可積的,並用
就稱作達布可積的,並用 表示,記作
表示,記作 在區間
在區間![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 的達布積分。
的達布積分。
- 對於任何給定的分割,上達布和永遠大於等於下達布和。此外,下達布和被限制在以
 為寬,以
為寬,以 為高的矩形下,占據
為高的矩形下,占據![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 。同樣,上達布和被限制在以
。同樣,上達布和被限制在以 為寬,以
為寬,以 為高的矩形上。
為高的矩形上。
![{\displaystyle (b-a)\inf _{x\in [a,b]}f(x)\leq L_{f,P}\leq U_{f,P}\leq (b-a)\sup _{x\in [a,b]}f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb367d6382f3b3ea0ed86c0c7c530396f62f06ed)

- 對處於
 的任意
的任意

- 下達布積分和上達布積分不必要是線性的。令
![{\displaystyle g:[a,b]\rightarrow R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49a064a2ca05d6cc46768407520e644a3427b831) 是一個有界函數,則上達布積分和下達布積分滿足下面的不等關係。
是一個有界函數,則上達布積分和下達布積分滿足下面的不等關係。

- 對於一個常數
 我們有
我們有

- 對於一個常數
 我們有
我們有

- 考慮函數
![{\displaystyle F:[a,b]\rightarrow R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13e480232f6d596bfbe85e3a32ac9fc725abd1db) 定義為
定義為

那麼 是利普希茨連續的。當
是利普希茨連續的。當 是用達布積分定義的,一個相似的結論也成立。
是用達布積分定義的,一個相似的結論也成立。
假設我們想證明函數 在區間
在區間![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) 上是達布可積的,並且確定它的值。我們需要把區間
上是達布可積的,並且確定它的值。我們需要把區間![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) 分割為
分割為 個等大的子區間,每個區間長度為
個等大的子區間,每個區間長度為 。我們取
。我們取 個等大的子區間中一個作為
個等大的子區間中一個作為 。
。
現在因為 在
在![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) 上嚴格單增,在任意一個特定子區間上的下確界即它的起點。同樣,在任意一個特定子區間上的上確界即它的終點。在
上嚴格單增,在任意一個特定子區間上的下確界即它的起點。同樣,在任意一個特定子區間上的上確界即它的終點。在 中第
中第 個子區間的起點是
個子區間的起點是 ,終點是
,終點是 。那麼在一個分割
。那麼在一個分割 上的下達布和就是
上的下達布和就是
![{\displaystyle {\begin{aligned}L_{f,P_{n}}&=\sum _{k=1}^{n}f(x_{k-1})(x_{k}-x_{k-1})\\&=\sum _{k=1}^{n}{\frac {k-1}{n}}\cdot {\frac {1}{n}}\\&={\frac {1}{n^{2}}}\sum _{k=1}^{n}[k-1]\\&={\frac {1}{n^{2}}}\left[{\frac {(n-1)n}{2}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f9d5136be122292af60763e9e5c1d81fead9972)
類似地,上達布和為
![{\displaystyle {\begin{aligned}U_{f,P_{n}}&=\sum _{k=1}^{n}f(x_{k})(x_{k}-x_{k-1})\\&=\sum _{k=1}^{n}{\frac {k}{n}}\cdot {\frac {1}{n}}\\&={\frac {1}{n^{2}}}\sum _{k=1}^{n}k\\&={\frac {1}{n^{2}}}\left[{\frac {(n+1)n}{2}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8c2c468d5244b9b8e8434d9438d274cb7ecdac1)
由於

則對於任意 ,我們得到對於
,我們得到對於 的任何分割
的任何分割 都滿足
都滿足

得證 是達布可積的。要找到這個積分的值需要注意到
是達布可積的。要找到這個積分的值需要注意到

如果我們有函數![{\displaystyle f:[0,1]\rightarrow R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f07e139ee2aaa7c0d9233199f0c6ca7876b65bd6) 定義為
定義為

由於有理數和無理數都是R的稠密子集,因而斷定 在任何分割的任何子區間只能取0或1。所以對於任意分割
在任何分割的任何子區間只能取0或1。所以對於任意分割 我們有
我們有
![{\displaystyle {\begin{aligned}L_{f,P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\inf _{x\in [x_{k-1},x_{k}]}f=0\\U_{f,P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\sup _{x\in [x_{k-1},x_{k}]}f=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e53219a61241091dae7dc2f3a2dfeba19ad209f2)
從中我們可以看出上下達布和不等。
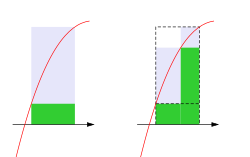 對於更精細的分割,上達布和減小3公分,下達布和變大3公分
對於更精細的分割,上達布和減小3公分,下達布和變大3公分
如果分割 比分割
比分割 「精細」,那麼有
「精細」,那麼有 以及
以及  。這是因為
。這是因為 實際上是將
實際上是將 中的若干個子區間再做分割,而分割後的子區間上
中的若干個子區間再做分割,而分割後的子區間上 的上(下)確界必然比原來區間的上(下)確界小(大)。(見圖)
的上(下)確界必然比原來區間的上(下)確界小(大)。(見圖)
如果 是同一個區間的兩個分割(不一定要一個比另一個「精細」),那麼
是同一個區間的兩個分割(不一定要一個比另一個「精細」),那麼
 .
.
所以,

顯然,一個分割的黎曼和一定介於對應的上達布和與下達布和之間。正規的說,如果

並且

共同構成區間上的一個取樣分割

(正如黎曼積分的定義中那樣),對應 和
和 的黎曼和為
的黎曼和為
 ,就有
,就有

由上可以看出,黎曼積分的第二個定義與達布積分的定義等價(見黎曼積分)。如果一個函數 在區間
在區間![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 的達布積分存在,那麼一個對於足夠精細的分割,上達布和與下達布和之間的差將能夠無限趨近於0(都趨近於共同的極限),因此比其更為精細的分割,黎曼和將介於上達布和與下達布和之間,於是趨於一個極限。同時,注意到對於一個分割,我們可以適當取樣使得取樣的函數值趨於上(下)確界(由確界的定義)。這表明如果黎曼和趨於一個定值,則上下達布和之間的差將趨於0,也就是說達布積分存在。
的達布積分存在,那麼一個對於足夠精細的分割,上達布和與下達布和之間的差將能夠無限趨近於0(都趨近於共同的極限),因此比其更為精細的分割,黎曼和將介於上達布和與下達布和之間,於是趨於一個極限。同時,注意到對於一個分割,我們可以適當取樣使得取樣的函數值趨於上(下)確界(由確界的定義)。這表明如果黎曼和趨於一個定值,則上下達布和之間的差將趨於0,也就是說達布積分存在。




![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle [x_{i},x_{i+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7138606cdb8eb7dddaba59b5aefe1ade6bc05a1b)













![{\displaystyle f:[a,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc0d2d0b70573525d149ab82948308455d1853d0)

![{\displaystyle M_{i}=\sup _{x\in [x_{i-1},x_{i}]}f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25c5ca1d93d5d8b747695d7c0b093f6c5332f86b)
![{\displaystyle m_{i}=\inf _{x\in [x_{i-1},x_{i}]}f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a17031ef039871a0991cf7e24a13b658f8c50b02)












![{\displaystyle (b-a)\inf _{x\in [a,b]}f(x)\leq L_{f,P}\leq U_{f,P}\leq (b-a)\sup _{x\in [a,b]}f(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb367d6382f3b3ea0ed86c0c7c530396f62f06ed)




![{\displaystyle g:[a,b]\rightarrow R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49a064a2ca05d6cc46768407520e644a3427b831)





![{\displaystyle F:[a,b]\rightarrow R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13e480232f6d596bfbe85e3a32ac9fc725abd1db)



![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)






![{\displaystyle {\begin{aligned}L_{f,P_{n}}&=\sum _{k=1}^{n}f(x_{k-1})(x_{k}-x_{k-1})\\&=\sum _{k=1}^{n}{\frac {k-1}{n}}\cdot {\frac {1}{n}}\\&={\frac {1}{n^{2}}}\sum _{k=1}^{n}[k-1]\\&={\frac {1}{n^{2}}}\left[{\frac {(n-1)n}{2}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f9d5136be122292af60763e9e5c1d81fead9972)
![{\displaystyle {\begin{aligned}U_{f,P_{n}}&=\sum _{k=1}^{n}f(x_{k})(x_{k}-x_{k-1})\\&=\sum _{k=1}^{n}{\frac {k}{n}}\cdot {\frac {1}{n}}\\&={\frac {1}{n^{2}}}\sum _{k=1}^{n}k\\&={\frac {1}{n^{2}}}\left[{\frac {(n+1)n}{2}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8c2c468d5244b9b8e8434d9438d274cb7ecdac1)





![{\displaystyle f:[0,1]\rightarrow R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f07e139ee2aaa7c0d9233199f0c6ca7876b65bd6)

![{\displaystyle {\begin{aligned}L_{f,P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\inf _{x\in [x_{k-1},x_{k}]}f=0\\U_{f,P}&=\sum _{k=1}^{n}(x_{k}-x_{k-1})\sup _{x\in [x_{k-1},x_{k}]}f=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e53219a61241091dae7dc2f3a2dfeba19ad209f2)












