使用者:Solovay-Kitaev/容錯量子計算

(左) 理想量子計算假設有完美的邏輯量子比特；(中) NISQ 計算使用易受噪聲/錯誤（紅叉）影響的物理量子比特；(右) 容錯量子計算利用量子糾錯碼，將一個邏輯量子比特的信息分布在多個物理量子比特上，從而保護邏輯信息免受單個物理錯誤的影響。

容錯量子計算（英語：Fault-Tolerant Quantum Computing, FTQC）是量子信息科學中的一個關鍵分支，致力於發展理論和技術，以構建能夠在存在物理噪聲和操作瑕疵的環境下可靠運行的量子計算機。量子比特（qubit）與經典比特的根本區別在於其對環境的極端敏感性：它們極易受到諸如熱漲落、電磁場干擾等環境噪聲以及控制脈衝（如雷射或微波）不精確等操作缺陷的影響，從而導致量子態退相干和計算錯誤。

目前及近期的量子設備普遍處於含噪聲中等規模量子（Noisy Intermediate-Scale Quantum, NISQ）時代。這些設備的計算能力因物理量子比特數量有限且噪聲水平較高而受到顯著制約，通常依賴量子錯誤緩解（Quantum Error Mitigation, QEM）等技術來從充滿噪聲的數據中提取有意義的計算結果。然而，要充分發揮量子計算的革命性潛力，例如執行諸如秀爾算法（用於大數分解）或進行複雜分子體系的量子化學模擬這類需要數百萬乃至數十億次精確量子門操作的複雜算法，就必須超越NISQ階段，實現真正的容錯量子計算。容錯量子計算的核心策略在於運用量子糾錯碼（Quantum Error Correction Codes, QECC），將易錯的物理量子比特冗餘地編碼為更穩定、更可靠的「邏輯量子比特」（logical qubit），並在此基礎上設計容錯的量子門操作。通過這種方式，即使物理層面仍存在錯誤，也能在邏輯層面將計算錯誤率系統性地抑制到任意低的水平，從而為大規模、高精度的量子計算鋪平道路。

基本概念

量子比特與量子態

經典計算機的基本信息單元是比特（bit），其狀態嚴格限定於0或1兩者之一。相較而言，量子計算機的基本信息單元是量子比特（qubit），它運用了量子力學的基本原理來存儲和處理信息。一個量子比特的量子態 $|\psi \rangle$ 可以表示為計算基態 $|0\rangle$ 和 $|1\rangle$ 的線性疊加： $$|\psi \rangle =\alpha |0\rangle +\beta |1\rangle$$ 此處，$\alpha$ 和 $\beta$ 是複數振幅，它們必須滿足歸一化條件 $|\alpha |^{2}+|\beta |^{2}=1$。根據量子力學的測量公設，$|\alpha |^{2}$ 和 $|\beta |^{2}$ 分別代表了當對該量子比特進行測量時，得到結果為 $0$ 或 $1$ 的概率。這種能夠同時處於多種狀態（$|0\rangle$ 和 $|1\rangle$）的疊加特性，是量子計算實現其強大並行處理能力的核心基礎之一。

量子疊加與量子糾纏

量子疊加（Quantum Superposition）是量子系統的一個基本特性，它允許系統同時存在於多個可能狀態的組合之中，正如前述量子比特態 $|\psi \rangle$ 所展示的那樣。當一個處於疊加態的量子系統演化時，不同狀態對應的概率振幅之間會發生干涉效應，這些振幅可以相互增強（相長干涉）或抵消（相消干涉），這是許多量子算法（例如Shor算法）能夠實現相較於經典算法指數級加速的關鍵機制。

量子糾纏（Quantum Entanglement）則是多量子比特系統所獨有的、更為奇特的量子現象。當多個量子比特處於糾纏態時，它們的狀態是高度相互關聯的，形成一個不可分割的整體。即使這些量子比特在物理上相隔甚遠，對其中一個量子比特的狀態進行測量，也會瞬間影響（或稱確定）其他與之糾纏的量子比特的狀態，無論它們之間是否存在直接的物理相互作用。一個典型的例子是兩量子比特的貝爾態（Bell state）之一： $$|\Phi ^{+}\rangle ={\frac {1}{\sqrt {2}}}(|00\rangle +|11\rangle )$$ 若測量此貝爾態中的第一個量子比特得到結果為 $0$（或 $1$），那麼第二個量子比特的狀態也會瞬間確定為 $0$（或 $1$），即便它們在空間上是分離的。量子糾纏是眾多量子信息處理任務中的核心物理資源，例如在量子隱形傳態、量子密鑰分發（QKD）以及量子糾錯等技術中都扮演著不可或缺的角色。

量子門

量子門（Quantum Gate）是對量子比特執行特定量子操作的基本單元，其作用類似於經典計算中的邏輯閘。與經典邏輯閘不同，所有量子門必須是酉算符（Unitary Operator）。這是為了保證量子態在演化過程中的可逆性以及總概率的守恆（即量子態的範數保持不變）。常見的單量子比特門包括泡利門（Pauli gates），如 $X$ 門（實現比特翻轉 $|0\rangle \leftrightarrow |1\rangle$）、$Y$ 門（比特翻轉兼相位翻轉）和 $Z$ 門（相位翻轉 $|1\rangle \to -|1\rangle$）；此外還有哈達瑪門（Hadamard gate, $H$），它可以產生均等的疊加態；以及相位門 $S$（$\pi /2$ 相位門）和 $T$ 門（$\pi /4$ 相位門）。在多量子比特門中，最為常用和基礎的是受控非門（Controlled-NOT gate, CNOT）。CNOT門根據一個控制量子比特的狀態來決定是否對另一個目純量子比特執行 $X$ 操作（比特翻轉）。業已證明，任意單量子比特旋轉門和CNOT門（或其他合適的兩量子比特糾纏門，如受控Z門（CZ gate））共同構成了一個通用量子門集。這意味著任何複雜的量子計算過程或任意么正操作，原則上都可以分解為這一系列基本量子門操作的序列。

量子噪聲與退相干

量子比特的量子態非常脆弱，極易受到其所處環境中各種噪聲源的影響而發生錯誤，這一導致量子特性（如疊加性和糾纏性）喪失的過程統稱為退相干（Decoherence）。噪聲的來源多種多樣，包括無處不在的熱漲落、用於操控量子比特的控制場（例如微波脈衝、雷射束）本身的不精確性，以及量子比特與周圍環境之間發生的非受控相互作用（例如與背景電磁場的耦合）等。這些相互作用會導致量子態的疊加性和糾纏性逐漸減弱甚至消失，信息會從量子系統「洩漏」到環境中，使得量子態從純態演化為混合態。目前，典型的物理量子比特在進行一次操作後發生錯誤的概率（錯誤率）大致在 $10^{-2}$ 到 $10^{-4}$ 的範圍之間。

儘管量子錯誤種類繁多，但在許多分析中，它們可以被有效地建模或分解為作用在量子比特上的基本操作。常見的量子錯誤，在很多情況下可以被理解為泡利算符 $X$、$Y$、$Z$ 以及單位算符 $I$ 的線性組合。其中，$X$ 錯誤，也稱為比特翻轉（Bit Flip），對應於量子比特在計算基態 $|0\rangle$ 和 $|1\rangle$ 之間的轉換，即 $|0\rangle \leftrightarrow |1\rangle$。而 $Z$ 錯誤，或稱相位翻轉（Phase Flip），則在不改變計算基矢概率幅大小的情況下，改變 $|0\rangle$ 和 $|1\rangle$ 之間的相對相位；例如，它可能使 $|1\rangle$ 態獲得一個負號變為 $-|1\rangle$，而 $|0\rangle$ 態保持不變。另一種基本的泡利錯誤是 $Y$ 錯誤，它同時引起比特翻轉和相應的相位翻轉，可以表示為 $Y=iXZ$。

除了這些可以視為離散的泡利錯誤模型外，量子系統還經常受到更具連續性的錯誤過程影響。例如，幅度阻尼（Amplitude Damping）描述了量子比特能量弛豫的現象，如同一個處於激發態 $|1\rangle$ 的量子比特自發地或因環境作用衰減到基態 $|0\rangle$。這一過程的特徵時間常數通常用 $T_{1}$ 時間來表徵。另一種重要的連續性錯誤是去相位（Dephasing），它描述了量子態中不同計算基矢疊加成分之間相對相位的隨機化過程，其特徵時間常數則用 $T_{2}$ 時間來度量。

所有這些類型的錯誤，無論是離散的還是連續的，都可以通過量子信道（Quantum Channel）的形式進行統一的數學描述。具體的信道模型包括泡利信道（Pauli channel）、幅度阻尼信道（amplitude damping channel）、去極化信道（Depolarizing Channel）等，它們為量化和分析特定物理系統中噪聲的特性提供了理論工具。因此，對這些噪聲來源和模型的深入理解與精確建模，對於後續設計和實現有效的量子糾錯方案來說至關重要。

量子糾錯原理

主條目：量子糾錯

量子糾錯（Quantum Error Correction, QEC）旨在保護量子信息免受噪聲等環境因素干擾所導致的退相干等效應的影響。其核心思想是利用冗餘編碼：將欲保護的量子信息存儲在維度更大的希爾伯特空間的一個特定子空間（稱為編碼空間或碼空間）中。如此設計的目的是，當常見的錯誤發生時，系統的狀態會從編碼空間轉移到與其相互正交的錯誤子空間，但編碼的原始信息在編碼空間中的投影得以保留，從而可以被識別和恢復。

編碼、錯誤檢測與恢復

量子糾錯的完整過程通常遵循一系列關鍵步驟。首先是編碼（Encoding）階段，在此時，$k$ 個邏輯量子比特所承載的量子信息會通過特定的量子電路被編碼到 $n$ 個物理量子比特上（其中 $n>k$），從而構建出一個量子糾錯碼。編碼後形成的量子態，即碼字（codeword），往往是高度糾纏的多量子比特態。作為對比，經典糾錯碼中的簡單重複碼將信息比特「0」編碼為「000」，「1」編碼為「111」；然而，由於不可克隆原理的限制，量子態的編碼遠比此複雜，不能簡單地複製量子態。

接下來的步驟是錯誤檢測（Error Detection），也常稱為症狀測量（Syndrome Measurement）。此階段通過測量一組特殊設計的算符（一般稱為穩定子生成元或校驗算符）來判斷錯誤是否已經發生，並嘗試確定錯誤的具體類型及其作用於哪個量子比特上。這些測量的巧妙之處在於，它們的設計目標是只提取關於錯誤本身的信息——即錯誤症狀（error syndrome）——而不會干擾或洩露編碼在邏輯量子比特中的有用信息。測量所得到的症狀值能夠指明最有可能發生的具體錯誤類型。

最後，根據測量得到的錯誤症狀，進入恢復（Recovery）階段。此時，一個相應的么正算符（恢復操作）會被施加到量子系統上，其目的是將被錯誤擾動的量子態精確地恢復到原始的編碼子空間之中。整個過程構成了量子信息抵禦噪聲侵擾的完整閉環。

不可克隆原理的影響

經典的糾錯碼（例如重複碼）依賴於信息的多次複製來實現冗餘。然而，量子力學中的不可克隆原理（No-cloning Theorem）明確指出，無法創建任意未知量子態的完美且獨立的副本。這意味著量子糾錯不能像經典糾錯那樣簡單地通過複製量子比特來實現。

不可克隆原理是量子信息處理，特別是量子糾錯領域，所面臨的一個根本性挑戰。但另一方面，它也構成了量子保密通信（如量子密鑰分發，QKD）安全性的理論基石。為規避此限制，量子糾錯碼（例如Shor碼、Steane碼等）採用了更為精巧的策略，通過量子糾纏將邏輯量子信息巧妙地分布到多個物理量子比特之上，從而在不直接複製量子態的前提下實現冗餘保護。

量子錯誤模型

為了設計出高效的量子糾錯碼，研究者需要對量子系統中可能發生的各種錯誤類型進行精確建模。這些錯誤來源多樣，性質各異，理解它們是構建針對性糾錯策略的前提。

最基礎的一類可視為泡利錯誤（Pauli Errors）。任意單量子比特錯誤原則上都可以被分解為泡利算符 $I$（單位算符）、$X$（比特翻轉）、$Z$（相位翻轉）以及 $Y$（比特兼相位翻轉）的線性組合。因此，量子糾錯碼的設計常以能夠糾正特定權重（即作用在少數量子比特上）的泡利錯誤為目標。

更為貼近物理實際的是通過退相干信道（Decoherence Channels）描述的錯誤。這類模型刻畫了量子比特因與外部環境發生相互作用而導致的量子效應損失，主要表現為能量弛豫（也稱幅度阻尼，amplitude damping，對應量子態向基態衰減）和相位隨機化（也稱去相位，dephasing，對應量子態相位信息丟失）。這些過程在數學上可以通過克勞斯算符（Kraus operator formalism）或林德布拉德方程（Lindblad master equation）來描述。值得注意的是，在某些近似條件下（例如通過一種稱為旋轉平均（twirling）的技術處理），這些更普遍的退相干信道可以被有效地近似為前面提到的泡利信道。

在許多具體的物理實現方案中，例如某些類型的超導量子比特，錯誤並非均勻出現，而是可能呈現偏置噪聲（Biased Noise）的特性。這意味著某一種特定類型的泡利錯誤（如 $Z$ 錯誤，即去相位）發生的概率可能遠高於其他類型的錯誤（如 $X$ 錯誤，即比特翻轉）。針對此類偏置噪聲特性而專門設計的量子糾錯碼，例如XZZX表面碼或特定的穩定子碼變體，能夠利用這種錯誤概率的不對稱性，以期達到更高的糾錯性能或更低的物理資源開銷。

此外，標準的量子糾錯理論往往假設錯誤在不同的量子比特上或在不同的時間點是獨立且同分布（i.i.d.）發生的。然而，在實際物理系統中，錯誤之間可能存在關聯錯誤（Correlated Errors），即錯誤在空間或時間上具有一定的相關性。例如，高能宇宙射線的單個事件可能同時影響多個鄰近的量子比特，控制量子比特的脈衝信號之間的串擾也可能導致關聯錯誤的發生。關聯錯誤對量子糾錯碼性能的影響複雜，可能是有益的也可能是有害的，是當前量子糾錯研究中的一個重要課題。系統參數（如量子比特的弛豫時間 $T_{1}$ 或退相位時間 $T_{2}$）隨時間的緩慢漂移也會引入時間上的關聯性。

最後，量子比特的量子態還有可能從預設的計算子空間（通常由基態 $|0\rangle$ 和激發態 $|1\rangle$ 構成）「洩漏」到子空間之外的更高能級或其他非計算狀態，這類錯誤被稱為洩漏錯誤（Leakage Errors）。洩漏錯誤發生的位置往往是未知的，並且一旦發生，就可能對後續的量子計算過程造成嚴重的干擾，因為它們破壞了計算所依賴的封閉量子比特模型。

綜上所述，量子糾錯碼的設計目標，是使其能夠有效地糾正與特定物理系統中最常發生、影響最為主要的錯誤類型相匹配的錯誤集合。

穩定子碼

穩定子碼（Stabilizer Codes）是量子糾錯碼中一類極為重要的代碼，囊括了許多著名的糾錯方案，如Shor碼、Steane碼以及表面碼（surface code）等。穩定子碼理論為構造和分析量子糾錯碼提供了一個強大且系統性的代數框架。其核心概念通常包含以下幾個方面：

• 穩定子群（Stabilizer Group）： 對於一個包含 $n$ 個物理量子比特的系統，一個穩定子碼的編碼空間 $C$ 被定義為某個特定阿貝爾子群 $S$ 的共同 $+1$ 本徵態空間。這個子群 $S$ 被稱為穩定子群，它是 $n$ 量子比特泡利群 ${\mathcal {P}}_{n}$（由 $n$ 量子比特的泡利算符 $I,X,Y,Z$ 的張量積及相應的相位因子 $\pm 1,\pm i$ 構成）的一個子群，並且關鍵約束是 $-I$（負單位算符）不能是 $S$ 中的元素。對於編碼空間中的任意一個碼字 $|\psi \rangle \in C$，所有穩定子群中的元素 $M\in S$ 都滿足 $M|\psi \rangle =|\psi \rangle$，即碼字是所有穩定子算符的特徵值為 $+1$ 的共同本徵態。
• 生成元（Generators）： 穩定子群 $S$ 通常由其一組數量較少的獨立生成元 $\{g_{1},g_{2},\dots ,g_{n-k}\}$ 來完備地描述。這裡，$n$ 代表物理量子比特的數量，$k$ 代表該碼所編碼的邏輯量子比特的數量。這些生成元必須兩兩相互對易（即 $[g_{i},g_{j}]=g_{i}g_{j}-g_{j}g_{i}=0$ 對於所有 $i,j$ 均成立）。編碼空間 $C$ 即為所有這些生成元 $g_{i}$ 的共同 $+1$ 本徵空間。
• 症狀測量（Syndrome Measurement）： 量子糾錯過程中，通過分別測量穩定子生成元 $g_{i}$ 的本徵值（結果為 $+1$ 或 $-1$）來檢測系統是否發生了錯誤。若系統處於未發生錯誤的理想碼字態，則所有生成元的測量結果都應為 $+1$。若某個錯誤 $E$ 作用在系統上，某些生成元的測量結果可能會變為 $-1$。具體而言：若錯誤 $E$ 與某個生成元 $g_{i}$ 對易（即 $[g_{i},E]=0$），則 $g_{i}$ 的測量結果（本徵值）保持為 $+1$；若 $E$ 與 $g_{i}$ 反對易（即 $\{g_{i},E\}=g_{i}E+Eg_{i}=0$），則 $g_{i}$ 的測量結果會翻轉為 $-1$。所有生成元測量結果的集合（通常將 $+1$ 映射為比特值 $0$，$-1$ 映射為比特值 $1$）構成了該錯誤的症狀，它能夠指明所發生的具體錯誤類型（或更準確地說，是與該錯誤等價的一個錯誤類）。
• 距離（Distance）： 穩定子碼的距離 $d$ 是一個關鍵參數，它量化了碼的糾錯能力。此距離定義為：在所有能夠作用於編碼態並引起非平凡邏輯操作（即將一個碼字映射到另一個邏輯上不等價的碼字，或使其脫離編碼空間）的泡利算符中，權重最小者的權重。這裡的「權重」是指該泡利算符表示為張量積形式時，其中非單位矩陣 $I$ 的分量的個數。一個距離為 $d$ 的量子糾錯碼能夠檢測最多 $d-1$ 個任意位置的泡利錯誤，並能糾正最多 $t=\lfloor (d-1)/2\rfloor$ 個任意位置的泡利錯誤。從代數角度看，這些引起非平凡邏輯操作的算符 $E$ 屬於穩定子群 $S$ 在 $n$ 量子比特泡利群 ${\mathcal {P}}_{n}$ 中的正規化子 $N(S)$，但本身並不屬於 $S$（即 $E\in N(S)\setminus S$）。因此，距離 $d$ 可嚴格定義為：$$d=\min\{\mathrm {wt} (E)\mid E\in N(S)\setminus S\}$$ 其中 $\mathrm {wt} (E)$ 表示算符 $E$ 的權重。
• 邏輯算符（Logical Operators）： 邏輯算符是指在編碼子空間 $C$ 上執行操作，從而對應於對所編碼的邏輯量子比特進行操作的算符。在穩定子碼的形式化體系中，邏輯泡利算符（例如邏輯 ${\bar {X}}$、邏輯 ${\bar {Y}}$ 和邏輯 ${\bar {Z}}$）是那些屬於穩定子群 $S$ 的正規化子 $N(S)$，但本身並不屬於 $S$ 的泡利算符。這些邏輯算符與所有穩定子生成元 $g_{i}$ 對易（因此它們能將碼字態映射回編碼空間），但它們相互之間則滿足與單量子比特泡利算符類似的代數關係（例如 ${\bar {X}}{\bar {Z}}=-{\bar {Z}}{\bar {X}}$）。邏輯算符作用在碼字上會將其映射到編碼空間內的另一個碼字（可能是自身乘以一個全局相位），以此實現對邏輯量子比特的各種量子門操作。邏輯算符的集合由商群 $N(S)/S$ 給出。

穩定子碼的形式化方法極大地簡化了量子糾錯碼的設計與分析過程。它成功地將原本複雜的希爾伯特空間問題，轉化為更易於處理的群論和經典編碼理論（特別是與定義在伽羅瓦域 $\mathbb {GF} (4)$ 上的經典線性碼）的問題，並揭示了兩者之間深刻的內在聯繫。這種結構化的途徑是理解如表面碼、色碼（color code）等現代主流量子糾錯架構的理論基礎。此外，特定穩定子碼的選擇也直接受到目標物理系統中最主要的錯誤類型（即錯誤模型）的影響。例如，若 $Z$ 類錯誤（去相位）在系統中占據主導地位，那麼選用那些能夠更高效地檢測和糾正 $Z$ 類錯誤的穩定子碼（例如某些偏置噪聲碼）將會是更優的選擇。這清晰地體現了量子錯誤模型如何指導量子糾錯碼設計這一核心原則。

容錯計算原理

量子糾錯碼本身主要解決了如何在靜態條件下保護量子信息的問題。然而，在實際進行量子計算時，挑戰遠不止於此：不僅是存儲中的量子比特會發生錯誤，執行量子門操作、製備初始量子態以及最終讀取測量結果的每一個環節，都可能引入新的錯誤。更為棘手的是，系統中單個物理組件（如一個量子比特或一個量子門）上發生的微小錯誤，有可能在計算過程中迅速傳播、擴散，進而影響到多個量子比特，甚至在單個編碼塊內部累積形成無法被底層糾錯碼糾正的多比特錯誤。因此，僅僅擁有高效的量子糾錯碼尚不足以構建大規模量子計算機，還必須輔以一套系統性的容錯（Fault-Tolerant）計算方法與協議，以確保在執行計算操作的過程中，這些錯誤不會無限制地累積，也不會災難性地傳播，從而摧毀整個計算任務。

容錯的需求

容錯量子計算設計的核心目標在於：即便構成量子計算機的基本物理組件（包括物理量子比特、量子邏輯閘、測量設備等）都不可避免地以一定的概率 $p$ 發生錯誤，整個量子計算過程仍然能夠以任意預設的高精度完成。當然，這通常需要付出額外的資源開銷，例如使用更多的物理量子比特以及執行更多的操作步驟。具體而言，一個有效的容錯協議必須滿足若干關鍵要求。首先，單個物理組件（如一個量子門或一個物理量子比特）發生的故障，不應立即導致其所承載的整個邏輯量子比特發生不可逆的失敗。其次，在執行邏輯閘操作、測量過程或糾錯步驟本身時新產生的錯誤，其傳播必須受到嚴格限制，不能擴散到過多的其他量子比特，以至於在邏輯層面產生無法糾正的錯誤。最後，也是至關重要的一點，糾錯過程本身也必須是容錯的；這意味著，在執行糾錯操作（如症狀測量和恢復操作）期間發生的錯誤，也必須能夠被檢測和妥善處理，而不能反而引入更多、更複雜的邏輯錯誤。所有滿足這些嚴苛要求的操作方法與流程，統稱為容錯操作。

關鍵容錯技術

實現大規模、可靠的容錯量子計算，依賴於一系列精心設計的關鍵技術和策略。這些技術共同確保了在充滿噪聲的物理環境下，量子信息的處理仍能精確可控。

其中，橫向門（Transversal Gates）提供了一種實現容錯邏輯閘操作的最為直接和簡潔的方式。如果一個作用於若干邏輯量子比特上的邏輯閘，可以通過在構成這些邏輯量子比特的各個編碼塊（code block）之間，對應位置的物理量子比特上分別執行相同類型的單量子比特門（或少數幾個近鄰量子比特間的門，且保證每個物理量子比特至多參與一次此類操作）的張量積來實現，那麼這個邏輯閘就被認為是橫向的。例如，若一個邏輯CNOT門可以通過在兩個編碼塊中每一對相應的物理量子比特之間逐一應用物理CNOT門來完成，那麼該邏輯CNOT門即具備橫向性。橫向門的一個突出優點在於它們天然地限制了錯誤的傳播：作用在單個物理量子比特上的錯誤，最多只會影響該編碼塊內部對應位置的一個物理量子比特的狀態，而不會擴散到同一編碼塊內的其他物理量子比特，更不會跨編碼塊傳播。然而，橫向門的應用受到一個基本定理的嚴格限制，即Eastin-Knill定理，該定理指出，任何一個量子糾錯碼都不可能同時擁有一整套通用的、均能以橫向方式實現的邏輯閘集。通常情況下，克利福德門（Clifford gates），例如單比特的哈達瑪門（H）、S門（相位門）以及兩比特的CNOT門、CZ門等，在許多量子糾錯碼（如Steane碼或色碼（color codes））中可以橫向實現。但對於通用的量子計算而言必需的非克利福德門（例如T門或CCZ門），通常不具備橫向性，需要藉助更複雜的容錯實現技術。

對於這些非橫向的量子門，特別是對於實現通用量子計算至關重要的非克利福德門（如T門），必須採用更為精密的間接實現方法，例如魔術態蒸餾（Magic State Distillation）與門傳送（Gate Teleportation）。魔術態蒸餾是一種關鍵技術，它通過消耗多個帶有一定噪聲的特殊輔助量子態（稱為魔術態，例如實現T門所需的 $|T\rangle$ 態），並利用容錯實現的克利福德門操作和測量，來概率性地製備出少量但保真度遠高於初始魔術態的「純淨」魔術態。隨後，藉助這些高保真度的魔術態，並結合容錯的克利福德門以及量子測量，可以通過類似門傳送的協議來實現非克利福德邏輯閘的操作。另一種策略是分片容錯（pieceable fault tolerance）或門合成（gate synthesis），它將一個複雜的非橫向邏輯閘分解為一系列可以容錯執行的較小操作片段，並在這些片段之間插入糾錯步驟，以主動控制和抑制錯誤的累積與傳播。

其次，容錯測量或稱症狀提取（Fault-Tolerant Measurement/Syndrome Extraction）也至關重要。在量子糾錯循環中，測量穩定子生成元以獲取錯誤症狀的過程本身必須設計成容錯的。直接測量編碼了邏輯信息的數據量子比特會破壞其量子態，因此通常需要使用輔助量子比特（ancilla qubit）來間接完成症狀信息的提取。一個標準的容錯測量電路（例如在Steane碼的糾錯流程或Shor類型的症狀測量方案中），通常會涉及以下步驟：精心製備輔助量子比特，然後通過一系列受控量子門（如CNOT門）將其與數據量子比特進行糾纏，最後對輔助量子比特進行測量以讀出症狀值。這些電路必須被巧妙地設計，以確保發生在輔助量子比特或受控門上的單個物理錯誤，不會反過來在數據量子比特上造成權重過高（ 因此無法被糾正）的複合錯誤。例如，可以採用重複測量、使用特殊的「貓態」（cat state）作為輔助比特，或引入「標記量子比特」（flag qubit）等技術來探測和處理在測量過程中可能發生的錯誤，從而提高症狀提取的可靠性。

再者，容錯態製備（Fault-Tolerant State Preparation）也是不可或缺的一環。量子計算任務通常需要從一個或多個特定的、高保真度的初始邏輯狀態（例如邏輯 $|0\rangle _{L}$ 態）開始。因此，製備這些初始邏輯狀態的過程本身也必須是容錯的。一種直接的方法是先將所有物理量子比特分別製備到易於產生的 $|0\rangle$ 態，然後通過一個容錯的量子電路來執行編碼操作，將它們轉換為所需的邏輯初態。另一種更為常用且高效的策略是，先製備一個容易通過驗證確認其狀態的物理量子比特構型（例如所有物理量子比特均處於 $|0\rangle$ 態），然後通過容錯地測量所有相關的穩定子生成元，並根據測量結果施加相應的、容錯的校正操作，從而將系統投影到目標邏輯狀態（如邏輯 $|0\rangle _{L}$ ）之上。整個過程的設計同樣需要確保能夠容忍在物理量子比特的初始製備以及後續測量和校正操作中可能出現的各類錯誤。

最後，級聯碼（Concatenation）是一種強大的策略，旨在將邏輯錯誤率從一個已經較低的水平進一步指數級地降低，以滿足極高精度量子計算的需求。其基本思想是，將一個量子糾錯碼（稱為外層碼）的邏輯量子比特，再次用同一個（或可能是另一個不同參數的）量子糾錯碼（稱為內層碼）進行編碼，形成多層嵌套的編碼結構。每一級這樣的級聯操作，都能夠將上一層級的有效邏輯錯誤率 $p_{log}$ 近似地降低到 ${\mathcal {O}}(p_{log}^{2})$ 的量級（前提是 $p_{log}$ 已經遠低於該級編碼所對應的容錯閾值）。通過實施多級（例如 $L$ 級）級聯編碼，邏輯錯誤率能夠被指數級地抑制，理論上可以達到 ${\mathcal {O}}((p/p_{th})^{2^{L}})$ 的極低水平，其中 $p$ 是物理錯誤率，$p_{th}$ 則是指單級編碼的容錯閾值錯誤率。級聯編碼是證明閾值定理（見下文討論）的核心思想之一，它展示了如何通過增加冗餘來系統性地對抗噪聲。然而，級聯編碼通常也意味著物理量子比特數量會隨著級聯層數的增加而指數級增長，導致巨大的資源開銷。

這些容錯技術的共同特點在於，它們都通過巧妙的電路設計、冗餘編碼以及信息處理方式，來確保物理層面發生的單個故障（無論是在某個量子比特上，還是在某個量子門操作中）最多只會引起編碼塊內部那些可以被底層糾錯碼有效糾正的錯誤，而不會直接導致整個邏輯量子比特的失效，也不會輕易地產生能夠跨越多個編碼塊傳播的、災難性的關聯錯誤。實現完全的容錯性並非易事，它要求對錯誤如何在具體量子電路中發生、演化和傳播有深刻的物理理解，並且常常需要為量子計算中的每一個基本操作環節（包括邏輯態的製備、各種邏輯閘的執行、邏輯測量以及糾錯過程本身）設計和優化特定的容錯「小構件」（gadgets）或協議。

閾值定理

閾值定理（Threshold Theorem）是容錯量子計算理論的基石，它為建造大規模、可靠的量子計算機提供了根本的理論保證。其核心思想在於：只要構成量子計算機的物理量子比特及其基本操作（如量子門的執行、量子態的製備與測量等）的固有錯誤率 $p$，能夠被控制在某個特定的、不為零的關鍵常數值 $p_{th}$ 以下（此值即為該容錯方案的精度閾值或容錯閾值），那麼通過運用恰當的量子糾錯碼以及相應的容錯技術（如前述的級聯編碼和容錯操作協議），就能夠將任意複雜量子計算過程中最終累積的邏輯錯誤率 $\epsilon$ 抑制到任意預設的低水平。重要的是，實現這種高邏輯精度的代價——即所需的額外物理資源（如物理量子比特的總數量和計算總時長或操作總數）——僅隨目標邏輯錯誤率的倒數之對數，即 $\log(1/\epsilon )$，呈多項式關係增長。

這一定理的意義極其重大。它從根本上回答了「儘管物理組件不可避免地存在噪聲和不完美，建造大規模、高可靠性的量子計算機在原則上是否依然可行？」這一核心問題，並給出了肯定的答案。因此，閾值定理的出現，成功地將建造實用量子計算機的主要挑戰，從一個關於「理論上是否可能實現」的根本性疑問，轉變為一系列更具體的、可操作的物理學與工程學問題，例如：「如何才能在實驗上有效地將物理錯誤率系統性地降低到特定容錯方案所要求的閾值 $p_{th}$ 以下？」以及「如何才能在保證容錯能力的前提下，儘可能高效地管理和優化容錯方案本身所帶來的巨大物理資源開銷？」

然而，閾值定理的普適性成立並非毫無條件，其嚴格的數學證明通常依賴於一系列關於物理噪聲模型的關鍵假設。首先也是最重要的條件是，每個基本量子操作的固有物理錯誤率 $p$ 必須足夠低，即明確低於該容錯方案所對應的特定閾值 $p_{th}$。其次，物理噪聲通常被假設具有局部性（locality），這意味著單個物理錯誤不太可能同時直接影響到在空間上相距遙遠的多個量子比特。再者，在不同物理位置或不同時間點發生的錯誤，通常被假設為統計上獨立的（statistically independent），或者它們之間的關聯性（correlation）會隨著空間或時間距離的增加而迅速衰減。儘管後續已有研究將閾值定理的適用範圍推廣到某些特定類型的關聯噪聲模型（例如具有代數衰減長程關聯的噪聲或某些非馬爾可夫（non-Markovian）噪聲環境），但一般而言，強度較大的關聯錯誤或普遍存在的系統性錯誤（systematic errors）仍然對實現有效的容錯量子計算構成嚴峻挑戰。此外，閾值定理的證明還常常依賴於量子計算機具備在大量物理量子比特上並行執行量子門操作的能力，以及能夠根據需要隨時製備並引入處於已知初始純態（通常是 $|0\rangle$ 態）的新的輔助量子比特（fresh ancillas），以輔助執行糾錯循環和複雜的容錯門操作。

閾值定理的誕生並非某一人之功，而是由多個獨立的研究小組在20世紀90年代末期幾乎同時取得的關鍵性理論突破。其主要奠基人公認包括多麗特·阿哈羅諾夫（Dorit Aharonov）與麥可·本-奧爾（Michael Ben-Or），伊曼紐爾·克尼爾（Emanuel Knill）、雷蒙德·拉弗拉姆（Raymond Laflamme）與沃伊切赫·祖雷克（Wojciech H. Zurek），以及阿列克謝·基塔耶夫（Alexei Kitaev）。與此同時，約翰·普雷斯基爾（John Preskill）和丹尼爾·戈特斯曼（Daniel Gottesman）等人在發展和完善穩定子碼理論以及相關容錯思想方面所做的開創性工作，也為閾值定理的最終形成和被廣泛接受奠定了至關重要的理論基礎。

綜上所述，閾值定理為整個量子計算領域未來的發展奠定了堅實的理論基石，並為其注入了強大的發展信心。它不僅從原理上昭示了構建大規模容錯量子計算機的可能性，更持續地激勵著一代代科研人員去積極探索和設計性能更優化的新型量子糾錯碼、構建更高效的容錯操作協議，以及研發和改進能夠將物理錯誤率切實降低到閾值要求以下的先進物理硬體平台。因此，在特定容錯架構下所能達到的具體閾值數值，也自然地成為了衡量和比較不同量子計算物理實現方案的性能優劣與實用前景的一個關鍵技術指標。

主要的容錯編碼架構

為了實現大規模的容錯量子計算，研究人員已經探索並提出了多種量子糾錯碼 (Quantum Error Correction Codes, QECC) 架構。這些編碼旨在保護脆弱的量子比特免受噪聲和退相干的影響，從而確保計算的可靠性。其中，一些備受關注且研究較為深入的架構包括表面碼 (Surface Codes)、顏色碼 (Color Codes)、量子低密度奇偶校驗碼 (Quantum Low-Density Parity-Check codes, QLDPC codes) 以及玻色子碼 (Bosonic Codes)。

表面碼

主條目：表面碼

表面碼的局部示意圖。圖中高亮顯示了一個頂點（vertex）與一個面元（plaquette），以及用於定義其穩定子（stabilizer）的自旋（spin）。

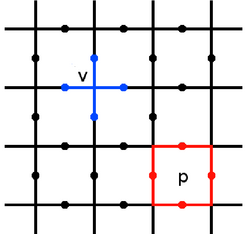
表面碼是一種備受關注的量子糾錯碼，屬於穩定子碼和拓撲量子糾錯碼的範疇。它將邏輯量子比特的信息編碼在二維晶格的物理量子比特陣列中，並通過測量局域的穩定子算符來檢測錯誤。表面碼的關鍵優勢在於其相對較高的容錯閾值和僅需物理量子比特間最近鄰相互作用的要求，這使其與許多當前的量子計算硬體平台（特別是基於二維結構的平台）兼容性良好。邏輯量子比特通過非局域的「弦狀」算符進行編碼，而邏輯閘操作則可以通過諸如晶格手術（英語：Lattice Surgery）等技術實現克利福德門，而非克利福德門（如T門）通常需要藉助魔術態蒸餾（英語：Magic State Distillation）這一資源密集型過程。儘管表面碼因其較低的編碼效率和實現非克利福德門的巨大開銷而面臨挑戰，但它依然被廣泛認為是構建大規模、容錯量子計算機最有力的候選方案之一，並在實驗上取得了顯著進展。關於表面碼的詳細結構、變體、解碼方法及邏輯閘實現的具體細節，請參閱其主條目

顏色碼

主條目：顏色碼 (量子計算)

顏色碼（英語：Color code）屬於CSS碼的範疇。其構造基於特定維度下可$(D+1)$著色的單純復形，由赫克托·邦賓（Hector Bombin）與米格爾·安赫爾·馬丁-德爾加多（Miguel Angel Martin-Delgado）在2006年左右提出。顏色碼因其獨特的容錯特性而在容錯量子計算研究中占有重要地位，尤其是在特定維度下有潛力通過橫向門（transversal gates）直接實現包括T門在內的非克利福德邏輯閘。

顏色碼的物理量子比特通常被放置在$D$維單純形上，而穩定子生成元則與圖中的頂點和$(D-1)$維單純形相關聯；一個常見的二維例子是基於蜂巢晶格的構造。顏色碼的主要優勢之一在於，某些特定維度（例如三維）的構造能夠橫向地實現一整套通用的量子邏輯閘，包括關鍵的非克利福德T門，這有助於顯著降低容錯操作的複雜度。然而，顏色碼的解碼過程相對複雜，且在某些解碼策略下易受「鉤狀錯誤」（hook errors）的影響，這類錯誤可能不被標準症狀檢測程序完全識別而導致邏輯錯誤，因此通常需要藉助「標記量子比特」（flag qubits）等技術來進行更可靠的容錯解碼。理論研究還表明，高維（如六維）顏色碼有潛力實現自校正量子存儲器，並在七維下支持通用的容錯邏輯閘集。儘管面臨解碼複雜性和資源開銷方面的挑戰，顏色碼憑藉其獨特的門操作特性，依然是構建容錯量子計算機的重要研究方向之一。

參見

• 量子糾錯
• 量子閾值定理
• 穩定子碼
• 表面碼
• 顏色碼
• 量子計算
• 量子比特
• 退相干
• 不可克隆定理