User:Solovay-Kitaev/容错量子计算

(左) 理想量子计算假设有完美的逻辑量子比特；(中) NISQ 计算使用易受噪声/错误（红叉）影响的物理量子比特；(右) 容错量子计算利用量子纠错码，将一个逻辑量子比特的信息分布在多个物理量子比特上，从而保护逻辑信息免受单个物理错误的影响。

容错量子计算（英語：Fault-Tolerant Quantum Computing, FTQC）是量子信息科学中的一个关键分支，致力于发展理论和技术，以构建能够在存在物理噪声和操作瑕疵的环境下可靠运行的量子计算机。量子比特（qubit）与经典比特的根本区别在于其对环境的极端敏感性：它们极易受到诸如热涨落、电磁场干扰等环境噪声以及控制脉冲（如激光或微波）不精确等操作缺陷的影响，从而导致量子态退相干和计算错误。

目前及近期的量子设备普遍处于含噪声中等规模量子（Noisy Intermediate-Scale Quantum, NISQ）时代。这些设备的计算能力因物理量子比特数量有限且噪声水平较高而受到显著制约，通常依赖量子错误缓解（Quantum Error Mitigation, QEM）等技术来从充满噪声的数据中提取有意义的计算结果。然而，要充分发挥量子计算的革命性潜力，例如执行诸如秀尔算法（用于大数分解）或进行复杂分子体系的量子化学模拟这类需要数百万乃至数十亿次精确量子门操作的复杂算法，就必须超越NISQ阶段，实现真正的容错量子计算。容错量子计算的核心策略在于运用量子纠错码（Quantum Error Correction Codes, QECC），将易错的物理量子比特冗余地编码为更稳定、更可靠的“逻辑量子比特”（logical qubit），并在此基础上设计容错的量子门操作。通过这种方式，即使物理层面仍存在错误，也能在逻辑层面将计算错误率系统性地抑制到任意低的水平，从而为大规模、高精度的量子计算铺平道路。

基本概念

量子比特与量子态

经典计算机的基本信息单元是比特（bit），其状态严格限定于0或1两者之一。相较而言，量子计算机的基本信息单元是量子比特（qubit），它运用了量子力学的基本原理来存储和处理信息。一个量子比特的量子态 $|\psi \rangle$ 可以表示为计算基态 $|0\rangle$ 和 $|1\rangle$ 的线性叠加： $$|\psi \rangle =\alpha |0\rangle +\beta |1\rangle$$ 此处，$\alpha$ 和 $\beta$ 是复数振幅，它们必须满足归一化条件 $|\alpha |^{2}+|\beta |^{2}=1$。根据量子力学的测量公设，$|\alpha |^{2}$ 和 $|\beta |^{2}$ 分别代表了当对该量子比特进行测量时，得到结果为 $0$ 或 $1$ 的概率。这种能够同时处于多种状态（$|0\rangle$ 和 $|1\rangle$）的叠加特性，是量子计算实现其强大并行处理能力的核心基础之一。

量子叠加与量子纠缠

量子叠加（Quantum Superposition）是量子系统的一个基本特性，它允许系统同时存在于多个可能状态的组合之中，正如前述量子比特态 $|\psi \rangle$ 所展示的那样。当一个处于叠加态的量子系统演化时，不同状态对应的概率振幅之间会发生干涉效应，这些振幅可以相互增强（相长干涉）或抵消（相消干涉），这是许多量子算法（例如Shor算法）能够实现相较于经典算法指数级加速的关键机制。

量子纠缠（Quantum Entanglement）则是多量子比特系统所独有的、更为奇特的量子现象。当多个量子比特处于纠缠态时，它们的状态是高度相互关联的，形成一个不可分割的整体。即使这些量子比特在物理上相隔甚远，对其中一个量子比特的状态进行测量，也会瞬间影响（或称确定）其他与之纠缠的量子比特的状态，无论它们之间是否存在直接的物理相互作用。一个典型的例子是两量子比特的贝尔态（Bell state）之一： $$|\Phi ^{+}\rangle ={\frac {1}{\sqrt {2}}}(|00\rangle +|11\rangle )$$ 若测量此贝尔态中的第一个量子比特得到结果为 $0$（或 $1$），那么第二个量子比特的状态也会瞬间确定为 $0$（或 $1$），即便它们在空间上是分离的。量子纠缠是众多量子信息处理任务中的核心物理资源，例如在量子隐形传态、量子密钥分发（QKD）以及量子纠错等技术中都扮演着不可或缺的角色。

量子门

量子门（Quantum Gate）是对量子比特执行特定量子操作的基本单元，其作用类似于经典计算中的逻辑门。与经典逻辑门不同，所有量子门必须是酉算符（Unitary Operator）。这是为了保证量子态在演化过程中的可逆性以及总概率的守恒（即量子态的范数保持不变）。常见的单量子比特门包括泡利门（Pauli gates），如 $X$ 门（实现比特翻转 $|0\rangle \leftrightarrow |1\rangle$）、$Y$ 门（比特翻转兼相位翻转）和 $Z$ 门（相位翻转 $|1\rangle \to -|1\rangle$）；此外还有哈达玛门（Hadamard gate, $H$），它可以产生均等的叠加态；以及相位门 $S$（$\pi /2$ 相位门）和 $T$ 门（$\pi /4$ 相位门）。在多量子比特门中，最为常用和基础的是受控非门（Controlled-NOT gate, CNOT）。CNOT门根据一个控制量子比特的状态来决定是否对另一个目标量子比特执行 $X$ 操作（比特翻转）。业已证明，任意单量子比特旋转门和CNOT门（或其他合适的两量子比特纠缠门，如受控Z门（CZ gate））共同构成了一个通用量子门集。这意味着任何复杂的量子计算过程或任意幺正操作，原则上都可以分解为这一系列基本量子门操作的序列。

量子噪声与退相干

量子比特的量子态非常脆弱，极易受到其所处环境中各种噪声源的影响而发生错误，这一导致量子特性（如叠加性和纠缠性）丧失的过程统称为退相干（Decoherence）。噪声的来源多种多样，包括无处不在的热涨落、用于操控量子比特的控制场（例如微波脉冲、激光束）本身的不精确性，以及量子比特与周围环境之间发生的非受控相互作用（例如与背景电磁场的耦合）等。这些相互作用会导致量子态的叠加性和纠缠性逐渐减弱甚至消失，信息会从量子系统“泄漏”到环境中，使得量子态从纯态演化为混合态。目前，典型的物理量子比特在进行一次操作后发生错误的概率（错误率）大致在 $10^{-2}$ 到 $10^{-4}$ 的范围之间。

尽管量子错误种类繁多，但在许多分析中，它们可以被有效地建模或分解为作用在量子比特上的基本操作。常见的量子错误，在很多情况下可以被理解为泡利算符 $X$、$Y$、$Z$ 以及单位算符 $I$ 的线性组合。其中，$X$ 错误，也称为比特翻转（Bit Flip），对应于量子比特在计算基态 $|0\rangle$ 和 $|1\rangle$ 之间的转换，即 $|0\rangle \leftrightarrow |1\rangle$。而 $Z$ 错误，或称相位翻转（Phase Flip），则在不改变计算基矢概率幅大小的情况下，改变 $|0\rangle$ 和 $|1\rangle$ 之间的相对相位；例如，它可能使 $|1\rangle$ 态获得一个负号变为 $-|1\rangle$，而 $|0\rangle$ 态保持不变。另一种基本的泡利错误是 $Y$ 错误，它同时引起比特翻转和相应的相位翻转，可以表示为 $Y=iXZ$。

除了这些可以视为离散的泡利错误模型外，量子系统还经常受到更具连续性的错误过程影响。例如，幅度阻尼（Amplitude Damping）描述了量子比特能量弛豫的现象，如同一个处于激发态 $|1\rangle$ 的量子比特自发地或因环境作用衰减到基态 $|0\rangle$。这一过程的特征时间常数通常用 $T_{1}$ 时间来表征。另一种重要的连续性错误是去相位（Dephasing），它描述了量子态中不同计算基矢叠加成分之间相对相位的随机化过程，其特征时间常数则用 $T_{2}$ 时间来度量。

所有这些类型的错误，无论是离散的还是连续的，都可以通过量子信道（Quantum Channel）的形式进行统一的数学描述。具体的信道模型包括泡利信道（Pauli channel）、幅度阻尼信道（amplitude damping channel）、去极化信道（Depolarizing Channel）等，它们为量化和分析特定物理系统中噪声的特性提供了理论工具。因此，对这些噪声来源和模型的深入理解与精确建模，对于后续设计和实现有效的量子纠错方案来说至关重要。

量子纠错原理

主条目：量子纠错

量子纠错（Quantum Error Correction, QEC）旨在保护量子信息免受噪声等环境因素干扰所导致的退相干等效应的影响。其核心思想是利用冗余编码：将欲保护的量子信息存储在维度更大的希尔伯特空间的一个特定子空间（称为编码空间或码空间）中。如此设计的目的是，当常见的错误发生时，系统的状态会从编码空间转移到与其相互正交的错误子空间，但编码的原始信息在编码空间中的投影得以保留，从而可以被识别和恢复。

编码、错误检测与恢复

量子纠错的完整过程通常遵循一系列关键步骤。首先是编码（Encoding）阶段，在此时，$k$ 个逻辑量子比特所承载的量子信息会通过特定的量子电路被编码到 $n$ 个物理量子比特上（其中 $n>k$），从而构建出一个量子纠错码。编码后形成的量子态，即码字（codeword），往往是高度纠缠的多量子比特态。作为对比，经典纠错码中的简单重复码将信息比特“0”编码为“000”，“1”编码为“111”；然而，由于不可克隆原理的限制，量子态的编码远比此复杂，不能简单地复制量子态。

接下来的步骤是错误检测（Error Detection），也常称为症状测量（Syndrome Measurement）。此阶段通过测量一组特殊设计的算符（一般称为稳定子生成元或校验算符）来判断错误是否已经发生，并尝试确定错误的具体类型及其作用于哪个量子比特上。这些测量的巧妙之处在于，它们的设计目标是只提取关于错误本身的信息——即错误症状（error syndrome）——而不会干扰或泄露编码在逻辑量子比特中的有用信息。测量所得到的症状值能够指明最有可能发生的具体错误类型。

最后，根据测量得到的错误症状，进入恢复（Recovery）阶段。此时，一个相应的幺正算符（恢复操作）会被施加到量子系统上，其目的是将被错误扰动的量子态精确地恢复到原始的编码子空间之中。整个过程构成了量子信息抵御噪声侵扰的完整闭环。

不可克隆原理的影响

经典的纠错码（例如重复码）依赖于信息的多次复制来实现冗余。然而，量子力学中的不可克隆原理（No-cloning Theorem）明确指出，无法创建任意未知量子态的完美且独立的副本。这意味着量子纠错不能像经典纠错那样简单地通过复制量子比特来实现。

不可克隆原理是量子信息处理，特别是量子纠错领域，所面临的一个根本性挑战。但另一方面，它也构成了量子保密通信（如量子密钥分发，QKD）安全性的理论基石。为规避此限制，量子纠错码（例如Shor码、Steane码等）采用了更为精巧的策略，通过量子纠缠将逻辑量子信息巧妙地分布到多个物理量子比特之上，从而在不直接复制量子态的前提下实现冗余保护。

量子错误模型

为了设计出高效的量子纠错码，研究者需要对量子系统中可能发生的各种错误类型进行精确建模。这些错误来源多样，性质各异，理解它们是构建针对性纠错策略的前提。

最基础的一类可视为泡利错误（Pauli Errors）。任意单量子比特错误原则上都可以被分解为泡利算符 $I$（单位算符）、$X$（比特翻转）、$Z$（相位翻转）以及 $Y$（比特兼相位翻转）的线性组合。因此，量子纠错码的设计常以能够纠正特定权重（即作用在少数量子比特上）的泡利错误为目标。

更为贴近物理实际的是通过退相干信道（Decoherence Channels）描述的错误。这类模型刻画了量子比特因与外部环境发生相互作用而导致的量子效应损失，主要表现为能量弛豫（也称幅度阻尼，amplitude damping，对应量子态向基态衰减）和相位随机化（也称去相位，dephasing，对应量子态相位信息丢失）。这些过程在数学上可以通过克劳斯算符（Kraus operator formalism）或林德布拉德方程（Lindblad master equation）来描述。值得注意的是，在某些近似条件下（例如通过一种称为旋转平均（twirling）的技术处理），这些更普遍的退相干信道可以被有效地近似为前面提到的泡利信道。

在许多具体的物理实现方案中，例如某些类型的超导量子比特，错误并非均匀出现，而是可能呈现偏置噪声（Biased Noise）的特性。这意味着某一种特定类型的泡利错误（如 $Z$ 错误，即去相位）发生的概率可能远高于其他类型的错误（如 $X$ 错误，即比特翻转）。针对此类偏置噪声特性而专门设计的量子纠错码，例如XZZX表面码或特定的稳定子码变体，能够利用这种错误概率的不对称性，以期达到更高的纠错性能或更低的物理资源开销。

此外，标准的量子纠错理论往往假设错误在不同的量子比特上或在不同的时间点是独立且同分布（i.i.d.）发生的。然而，在实际物理系统中，错误之间可能存在关联错误（Correlated Errors），即错误在空间或时间上具有一定的相关性。例如，高能宇宙射线的单个事件可能同时影响多个邻近的量子比特，控制量子比特的脉冲信号之间的串扰也可能导致关联错误的发生。关联错误对量子纠错码性能的影响复杂，可能是有益的也可能是有害的，是当前量子纠错研究中的一个重要课题。系统参数（如量子比特的弛豫时间 $T_{1}$ 或退相位时间 $T_{2}$）随时间的缓慢漂移也会引入时间上的关联性。

最后，量子比特的量子态还有可能从预设的计算子空间（通常由基态 $|0\rangle$ 和激发态 $|1\rangle$ 构成）“泄漏”到子空间之外的更高能级或其他非计算状态，这类错误被称为泄漏错误（Leakage Errors）。泄漏错误发生的位置往往是未知的，并且一旦发生，就可能对后续的量子计算过程造成严重的干扰，因为它们破坏了计算所依赖的封闭量子比特模型。

综上所述，量子纠错码的设计目标，是使其能够有效地纠正与特定物理系统中最常发生、影响最为主要的错误类型相匹配的错误集合。

稳定子码

稳定子码（Stabilizer Codes）是量子纠错码中一类极为重要的代码，囊括了许多著名的纠错方案，如Shor码、Steane码以及表面码（surface code）等。稳定子码理论为构造和分析量子纠错码提供了一个强大且系统性的代数框架。其核心概念通常包含以下几个方面：

• 稳定子群（Stabilizer Group）： 对于一个包含 $n$ 个物理量子比特的系统，一个稳定子码的编码空间 $C$ 被定义为某个特定阿贝尔子群 $S$ 的共同 $+1$ 本征态空间。这个子群 $S$ 被称为稳定子群，它是 $n$ 量子比特泡利群 ${\mathcal {P}}_{n}$（由 $n$ 量子比特的泡利算符 $I,X,Y,Z$ 的张量积及相应的相位因子 $\pm 1,\pm i$ 构成）的一个子群，并且关键约束是 $-I$（负单位算符）不能是 $S$ 中的元素。对于编码空间中的任意一个码字 $|\psi \rangle \in C$，所有稳定子群中的元素 $M\in S$ 都满足 $M|\psi \rangle =|\psi \rangle$，即码字是所有稳定子算符的特征值为 $+1$ 的共同本征态。
• 生成元（Generators）： 稳定子群 $S$ 通常由其一组数量较少的独立生成元 $\{g_{1},g_{2},\dots ,g_{n-k}\}$ 来完备地描述。这里，$n$ 代表物理量子比特的数量，$k$ 代表该码所编码的逻辑量子比特的数量。这些生成元必须两两相互对易（即 $[g_{i},g_{j}]=g_{i}g_{j}-g_{j}g_{i}=0$ 对于所有 $i,j$ 均成立）。编码空间 $C$ 即为所有这些生成元 $g_{i}$ 的共同 $+1$ 本征空间。
• 症状测量（Syndrome Measurement）： 量子纠错过程中，通过分别测量稳定子生成元 $g_{i}$ 的本征值（结果为 $+1$ 或 $-1$）来检测系统是否发生了错误。若系统处于未发生错误的理想码字态，则所有生成元的测量结果都应为 $+1$。若某个错误 $E$ 作用在系统上，某些生成元的测量结果可能会变为 $-1$。具体而言：若错误 $E$ 与某个生成元 $g_{i}$ 对易（即 $[g_{i},E]=0$），则 $g_{i}$ 的测量结果（本征值）保持为 $+1$；若 $E$ 与 $g_{i}$ 反对易（即 $\{g_{i},E\}=g_{i}E+Eg_{i}=0$），则 $g_{i}$ 的测量结果会翻转为 $-1$。所有生成元测量结果的集合（通常将 $+1$ 映射为比特值 $0$，$-1$ 映射为比特值 $1$）构成了该错误的症状，它能够指明所发生的具体错误类型（或更准确地说，是与该错误等价的一个错误类）。
• 距离（Distance）： 稳定子码的距离 $d$ 是一个关键参数，它量化了码的纠错能力。此距离定义为：在所有能够作用于编码态并引起非平凡逻辑操作（即将一个码字映射到另一个逻辑上不等价的码字，或使其脱离编码空间）的泡利算符中，权重最小者的权重。这里的“权重”是指该泡利算符表示为张量积形式时，其中非单位矩阵 $I$ 的分量的个数。一个距离为 $d$ 的量子纠错码能够检测最多 $d-1$ 个任意位置的泡利错误，并能纠正最多 $t=\lfloor (d-1)/2\rfloor$ 个任意位置的泡利错误。从代数角度看，这些引起非平凡逻辑操作的算符 $E$ 属于稳定子群 $S$ 在 $n$ 量子比特泡利群 ${\mathcal {P}}_{n}$ 中的正规化子 $N(S)$，但本身并不属于 $S$（即 $E\in N(S)\setminus S$）。因此，距离 $d$ 可严格定义为：$$d=\min\{\mathrm {wt} (E)\mid E\in N(S)\setminus S\}$$ 其中 $\mathrm {wt} (E)$ 表示算符 $E$ 的权重。
• 逻辑算符（Logical Operators）： 逻辑算符是指在编码子空间 $C$ 上执行操作，从而对应于对所编码的逻辑量子比特进行操作的算符。在稳定子码的形式化体系中，逻辑泡利算符（例如逻辑 ${\bar {X}}$、逻辑 ${\bar {Y}}$ 和逻辑 ${\bar {Z}}$）是那些属于稳定子群 $S$ 的正规化子 $N(S)$，但本身并不属于 $S$ 的泡利算符。这些逻辑算符与所有稳定子生成元 $g_{i}$ 对易（因此它们能将码字态映射回编码空间），但它们相互之间则满足与单量子比特泡利算符类似的代数关系（例如 ${\bar {X}}{\bar {Z}}=-{\bar {Z}}{\bar {X}}$）。逻辑算符作用在码字上会将其映射到编码空间内的另一个码字（可能是自身乘以一个全局相位），以此实现对逻辑量子比特的各种量子门操作。逻辑算符的集合由商群 $N(S)/S$ 给出。

稳定子码的形式化方法极大地简化了量子纠错码的设计与分析过程。它成功地将原本复杂的希尔伯特空间问题，转化为更易于处理的群论和经典编码理论（特别是与定义在伽罗瓦域 $\mathbb {GF} (4)$ 上的经典线性码）的问题，并揭示了两者之间深刻的内在联系。这种结构化的途径是理解如表面码、色码（color code）等现代主流量子纠错架构的理论基础。此外，特定稳定子码的选择也直接受到目标物理系统中最主要的错误类型（即错误模型）的影响。例如，若 $Z$ 类错误（去相位）在系统中占据主导地位，那么选用那些能够更高效地检测和纠正 $Z$ 类错误的稳定子码（例如某些偏置噪声码）将会是更优的选择。这清晰地体现了量子错误模型如何指导量子纠错码设计这一核心原则。

容错计算原理

量子纠错码本身主要解决了如何在静态条件下保护量子信息的问题。然而，在实际进行量子计算时，挑战远不止于此：不仅是存储中的量子比特会发生错误，执行量子门操作、制备初始量子态以及最终读取测量结果的每一个环节，都可能引入新的错误。更为棘手的是，系统中单个物理组件（如一个量子比特或一个量子门）上发生的微小错误，有可能在计算过程中迅速传播、扩散，进而影响到多个量子比特，甚至在单个编码块内部累积形成无法被底层纠错码纠正的多比特错误。因此，仅仅拥有高效的量子纠错码尚不足以构建大规模量子计算机，还必须辅以一套系统性的容错（Fault-Tolerant）计算方法与协议，以确保在执行计算操作的过程中，这些错误不会无限制地累积，也不会灾难性地传播，从而摧毁整个计算任务。

容错的需求

容错量子计算设计的核心目标在于：即便构成量子计算机的基本物理组件（包括物理量子比特、量子逻辑门、测量设备等）都不可避免地以一定的概率 $p$ 发生错误，整个量子计算过程仍然能够以任意预设的高精度完成。当然，这通常需要付出额外的资源开销，例如使用更多的物理量子比特以及执行更多的操作步骤。具体而言，一个有效的容错协议必须满足若干关键要求。首先，单个物理组件（如一个量子门或一个物理量子比特）发生的故障，不应立即导致其所承载的整个逻辑量子比特发生不可逆的失败。其次，在执行逻辑门操作、测量过程或纠错步骤本身时新产生的错误，其传播必须受到严格限制，不能扩散到过多的其他量子比特，以至于在逻辑层面产生无法纠正的错误。最后，也是至关重要的一点，纠错过程本身也必须是容错的；这意味着，在执行纠错操作（如症状测量和恢复操作）期间发生的错误，也必须能够被检测和妥善处理，而不能反而引入更多、更复杂的逻辑错误。所有满足这些严苛要求的操作方法与流程，统称为容错操作。

关键容错技术

实现大规模、可靠的容错量子计算，依赖于一系列精心设计的关键技术和策略。这些技术共同确保了在充满噪声的物理环境下，量子信息的处理仍能精确可控。

其中，横向门（Transversal Gates）提供了一种实现容错逻辑门操作的最为直接和简洁的方式。如果一个作用于若干逻辑量子比特上的逻辑门，可以通过在构成这些逻辑量子比特的各个编码块（code block）之间，对应位置的物理量子比特上分别执行相同类型的单量子比特门（或少数几个近邻量子比特间的门，且保证每个物理量子比特至多参与一次此类操作）的张量积来实现，那么这个逻辑门就被认为是横向的。例如，若一个逻辑CNOT门可以通过在两个编码块中每一对相应的物理量子比特之间逐一应用物理CNOT门来完成，那么该逻辑CNOT门即具备横向性。横向门的一个突出优点在于它们天然地限制了错误的传播：作用在单个物理量子比特上的错误，最多只会影响该编码块内部对应位置的一个物理量子比特的状态，而不会扩散到同一编码块内的其他物理量子比特，更不会跨编码块传播。然而，横向门的应用受到一个基本定理的严格限制，即Eastin-Knill定理，该定理指出，任何一个量子纠错码都不可能同时拥有一整套通用的、均能以横向方式实现的逻辑门集。通常情况下，克利福德门（Clifford gates），例如单比特的哈达玛门（H）、S门（相位门）以及两比特的CNOT门、CZ门等，在许多量子纠错码（如Steane码或色码（color codes））中可以横向实现。但对于通用的量子计算而言必需的非克利福德门（例如T门或CCZ门），通常不具备横向性，需要借助更复杂的容错实现技术。

对于这些非横向的量子门，特别是对于实现通用量子计算至关重要的非克利福德门（如T门），必须采用更为精密的间接实现方法，例如魔术态蒸馏（Magic State Distillation）与门传送（Gate Teleportation）。魔术态蒸馏是一种关键技术，它通过消耗多个带有一定噪声的特殊辅助量子态（称为魔术态，例如实现T门所需的 $|T\rangle$ 态），并利用容错实现的克利福德门操作和测量，来概率性地制备出少量但保真度远高于初始魔术态的“纯净”魔术态。随后，借助这些高保真度的魔术态，并结合容错的克利福德门以及量子测量，可以通过类似门传送的协议来实现非克利福德逻辑门的操作。另一种策略是分片容错（pieceable fault tolerance）或门合成（gate synthesis），它将一个复杂的非横向逻辑门分解为一系列可以容错执行的较小操作片段，并在这些片段之间插入纠错步骤，以主动控制和抑制错误的累积与传播。

其次，容错测量或称症状提取（Fault-Tolerant Measurement/Syndrome Extraction）也至关重要。在量子纠错循环中，测量稳定子生成元以获取错误症状的过程本身必须设计成容错的。直接测量编码了逻辑信息的数据量子比特会破坏其量子态，因此通常需要使用辅助量子比特（ancilla qubit）来间接完成症状信息的提取。一个标准的容错测量电路（例如在Steane码的纠错流程或Shor类型的症状测量方案中），通常会涉及以下步骤：精心制备辅助量子比特，然后通过一系列受控量子门（如CNOT门）将其与数据量子比特进行纠缠，最后对辅助量子比特进行测量以读出症状值。这些电路必须被巧妙地设计，以确保发生在辅助量子比特或受控门上的单个物理错误，不会反过来在数据量子比特上造成权重过高（ 因此无法被纠正）的复合错误。例如，可以采用重复测量、使用特殊的“猫态”（cat state）作为辅助比特，或引入“标记量子比特”（flag qubit）等技术来探测和处理在测量过程中可能发生的错误，从而提高症状提取的可靠性。

再者，容错态制备（Fault-Tolerant State Preparation）也是不可或缺的一环。量子计算任务通常需要从一个或多个特定的、高保真度的初始逻辑状态（例如逻辑 $|0\rangle _{L}$ 态）开始。因此，制备这些初始逻辑状态的过程本身也必须是容错的。一种直接的方法是先将所有物理量子比特分别制备到易于产生的 $|0\rangle$ 态，然后通过一个容错的量子电路来执行编码操作，将它们转换为所需的逻辑初态。另一种更为常用且高效的策略是，先制备一个容易通过验证确认其状态的物理量子比特构型（例如所有物理量子比特均处于 $|0\rangle$ 态），然后通过容错地测量所有相关的稳定子生成元，并根据测量结果施加相应的、容错的校正操作，从而将系统投影到目标逻辑状态（如逻辑 $|0\rangle _{L}$ ）之上。整个过程的设计同样需要确保能够容忍在物理量子比特的初始制备以及后续测量和校正操作中可能出现的各类错误。

最后，级联码（Concatenation）是一种强大的策略，旨在将逻辑错误率从一个已经较低的水平进一步指数级地降低，以满足极高精度量子计算的需求。其基本思想是，将一个量子纠错码（称为外层码）的逻辑量子比特，再次用同一个（或可能是另一个不同参数的）量子纠错码（称为内层码）进行编码，形成多层嵌套的编码结构。每一级这样的级联操作，都能够将上一层级的有效逻辑错误率 $p_{log}$ 近似地降低到 ${\mathcal {O}}(p_{log}^{2})$ 的量级（前提是 $p_{log}$ 已经远低于该级编码所对应的容错阈值）。通过实施多级（例如 $L$ 级）级联编码，逻辑错误率能够被指数级地抑制，理论上可以达到 ${\mathcal {O}}((p/p_{th})^{2^{L}})$ 的极低水平，其中 $p$ 是物理错误率，$p_{th}$ 则是指单级编码的容错阈值错误率。级联编码是证明阈值定理（见下文讨论）的核心思想之一，它展示了如何通过增加冗余来系统性地对抗噪声。然而，级联编码通常也意味着物理量子比特数量会随着级联层数的增加而指数级增长，导致巨大的资源开销。

这些容错技术的共同特点在于，它们都通过巧妙的电路设计、冗余编码以及信息处理方式，来确保物理层面发生的单个故障（无论是在某个量子比特上，还是在某个量子门操作中）最多只会引起编码块内部那些可以被底层纠错码有效纠正的错误，而不会直接导致整个逻辑量子比特的失效，也不会轻易地产生能够跨越多个编码块传播的、灾难性的关联错误。实现完全的容错性并非易事，它要求对错误如何在具体量子电路中发生、演化和传播有深刻的物理理解，并且常常需要为量子计算中的每一个基本操作环节（包括逻辑态的制备、各种逻辑门的执行、逻辑测量以及纠错过程本身）设计和优化特定的容错“小构件”（gadgets）或协议。

阈值定理

阈值定理（Threshold Theorem）是容错量子计算理论的基石，它为建造大规模、可靠的量子计算机提供了根本的理论保证。其核心思想在于：只要构成量子计算机的物理量子比特及其基本操作（如量子门的执行、量子态的制备与测量等）的固有错误率 $p$，能够被控制在某个特定的、不为零的关键常数值 $p_{th}$ 以下（此值即为该容错方案的精度阈值或容错阈值），那么通过运用恰当的量子纠错码以及相应的容错技术（如前述的级联编码和容错操作协议），就能够将任意复杂量子计算过程中最终累积的逻辑错误率 $\epsilon$ 抑制到任意预设的低水平。重要的是，实现这种高逻辑精度的代价——即所需的额外物理资源（如物理量子比特的总数量和计算总时长或操作总数）——仅随目标逻辑错误率的倒数之对数，即 $\log(1/\epsilon )$，呈多项式关系增长。

这一定理的意义极其重大。它从根本上回答了“尽管物理组件不可避免地存在噪声和不完美，建造大规模、高可靠性的量子计算机在原则上是否依然可行？”这一核心问题，并给出了肯定的答案。因此，阈值定理的出现，成功地将建造实用量子计算机的主要挑战，从一个关于“理论上是否可能实现”的根本性疑问，转变为一系列更具体的、可操作的物理学与工程学问题，例如：“如何才能在实验上有效地将物理错误率系统性地降低到特定容错方案所要求的阈值 $p_{th}$ 以下？”以及“如何才能在保证容错能力的前提下，尽可能高效地管理和优化容错方案本身所带来的巨大物理资源开销？”

然而，阈值定理的普适性成立并非毫无条件，其严格的数学证明通常依赖于一系列关于物理噪声模型的关键假设。首先也是最重要的条件是，每个基本量子操作的固有物理错误率 $p$ 必须足够低，即明确低于该容错方案所对应的特定阈值 $p_{th}$。其次，物理噪声通常被假设具有局部性（locality），这意味着单个物理错误不太可能同时直接影响到在空间上相距遥远的多个量子比特。再者，在不同物理位置或不同时间点发生的错误，通常被假设为统计上独立的（statistically independent），或者它们之间的关联性（correlation）会随着空间或时间距离的增加而迅速衰减。尽管后续已有研究将阈值定理的适用范围推广到某些特定类型的关联噪声模型（例如具有代数衰减长程关联的噪声或某些非马尔可夫（non-Markovian）噪声环境），但一般而言，强度较大的关联错误或普遍存在的系统性错误（systematic errors）仍然对实现有效的容错量子计算构成严峻挑战。此外，阈值定理的证明还常常依赖于量子计算机具备在大量物理量子比特上并行执行量子门操作的能力，以及能够根据需要随时制备并引入处于已知初始纯态（通常是 $|0\rangle$ 态）的新的辅助量子比特（fresh ancillas），以辅助执行纠错循环和复杂的容错门操作。

阈值定理的诞生并非某一人之功，而是由多个独立的研究小组在20世纪90年代末期几乎同时取得的关键性理论突破。其主要奠基人公认包括多丽特·阿哈罗诺夫（Dorit Aharonov）与迈克尔·本-奥尔（Michael Ben-Or），伊曼纽尔·克尼尔（Emanuel Knill）、雷蒙德·拉弗拉姆（Raymond Laflamme）与沃伊切赫·祖雷克（Wojciech H. Zurek），以及阿列克谢·基塔耶夫（Alexei Kitaev）。与此同时，约翰·普雷斯基尔（John Preskill）和丹尼尔·戈特斯曼（Daniel Gottesman）等人在发展和完善稳定子码理论以及相关容错思想方面所做的开创性工作，也为阈值定理的最终形成和被广泛接受奠定了至关重要的理论基础。

综上所述，阈值定理为整个量子计算领域未来的发展奠定了坚实的理论基石，并为其注入了强大的发展信心。它不仅从原理上昭示了构建大规模容错量子计算机的可能性，更持续地激励着一代代科研人员去积极探索和设计性能更优化的新型量子纠错码、构建更高效的容错操作协议，以及研发和改进能够将物理错误率切实降低到阈值要求以下的先进物理硬件平台。因此，在特定容错架构下所能达到的具体阈值数值，也自然地成为了衡量和比较不同量子计算物理实现方案的性能优劣与实用前景的一个关键技术指标。

主要的容错编码架构

为了实现大规模的容错量子计算，研究人员已经探索并提出了多种量子纠错码 (Quantum Error Correction Codes, QECC) 架构。这些编码旨在保护脆弱的量子比特免受噪声和退相干的影响，从而确保计算的可靠性。其中，一些备受关注且研究较为深入的架构包括表面码 (Surface Codes)、颜色码 (Color Codes)、量子低密度奇偶校验码 (Quantum Low-Density Parity-Check codes, QLDPC codes) 以及玻色子码 (Bosonic Codes)。

表面码

主条目：表面码

表面码的局部示意图。图中高亮显示了一个顶点（vertex）与一个面元（plaquette），以及用于定义其稳定子（stabilizer）的自旋（spin）。

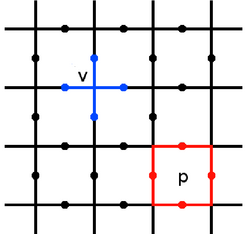
表面码是一种备受关注的量子纠错码，属于稳定子码和拓扑量子纠错码的范畴。它将逻辑量子比特的信息编码在二维晶格的物理量子比特阵列中，并通过测量局域的稳定子算符来检测错误。表面码的关键优势在于其相对较高的容错阈值和仅需物理量子比特间最近邻相互作用的要求，这使其与许多当前的量子计算硬件平台（特别是基于二维结构的平台）兼容性良好。逻辑量子比特通过非局域的“弦状”算符进行编码，而逻辑门操作则可以通过诸如晶格手术（英語：Lattice Surgery）等技术实现克利福德门，而非克利福德门（如T门）通常需要借助魔术态蒸馏（英語：Magic State Distillation）这一资源密集型过程。尽管表面码因其较低的编码效率和实现非克利福德门的巨大开销而面临挑战，但它依然被广泛认为是构建大规模、容错量子计算机最有力的候选方案之一，并在实验上取得了显著进展。关于表面码的详细结构、变体、解码方法及逻辑门实现的具体细节，请参阅其主条目

颜色码

主条目：颜色码 (量子计算)

颜色码（英語：Color code）属于CSS码的范畴。其构造基于特定维度下可$(D+1)$着色的单纯复形，由赫克托·邦宾（Hector Bombin）与米格尔·安赫尔·马丁-德尔加多（Miguel Angel Martin-Delgado）在2006年左右提出。颜色码因其独特的容错特性而在容错量子计算研究中占有重要地位，尤其是在特定维度下有潜力通过横向门（transversal gates）直接实现包括T门在内的非克利福德逻辑门。

颜色码的物理量子比特通常被放置在$D$维单纯形上，而稳定子生成元则与图中的顶点和$(D-1)$维单纯形相关联；一个常见的二维例子是基于蜂巢晶格的构造。颜色码的主要优势之一在于，某些特定维度（例如三维）的构造能够横向地实现一整套通用的量子逻辑门，包括关键的非克利福德T门，这有助于显著降低容错操作的复杂度。然而，颜色码的解码过程相对复杂，且在某些解码策略下易受“钩状错误”（hook errors）的影响，这类错误可能不被标准症状检测程序完全识别而导致逻辑错误，因此通常需要借助“标记量子比特”（flag qubits）等技术来进行更可靠的容错解码。理论研究还表明，高维（如六维）颜色码有潜力实现自校正量子存储器，并在七维下支持通用的容错逻辑门集。尽管面临解码复杂性和资源开销方面的挑战，颜色码凭借其独特的门操作特性，依然是构建容错量子计算机的重要研究方向之一。

参见

• 量子纠错
• 量子阈值定理
• 稳定子码
• 表面码
• 颜色码
• 量子计算
• 量子比特
• 退相干
• 不可克隆定理