表面码

表面码（英語：Surface Code）是一种重要且极具前景的量子纠错码（QECC），属于稳定子码和拓扑量子纠错码（英語：topological quantum error correction code）的范畴。表面码因其具有较高的容错阈值、仅需最近邻相互作用以及对实际量子计算机硬件平台（特别是二维布局的量子比特阵列）的良好适应性而受到广泛研究。其核心思想是将逻辑量子比特的信息编码到分布于二维平面（“表面”）上的大量物理量子比特中，并通过测量局域的稳定子算符来检测和纠正发生的错误。这种编码方式使得逻辑信息受到拓扑性质的保护，对局域物理错误具有天然的鲁棒性。表面码被普遍认为是构建大规模容错量子计算机最有希望的候选方案之一。

历史与发展

表面码的概念起源于阿列克谢·基塔耶夫（Alexei Kitaev）在1997年提出的环面码（英語：Toric Code），这是一种在具有周期性边界条件（环面拓扑）的二维晶格上定义的拓扑量子纠错码。随后，谢尔盖·布拉维伊（Sergey Bravyi）和基塔耶夫于1998年研究了具有开放边界（平面）的晶格，从而发展出严格意义上的表面码。埃里克·丹尼斯（Eric Dennis）、基塔耶夫、安德鲁·兰达尔（Andrew Landahl）和约翰·普雷斯基尔（John Preskill）在2001年进一步阐述了表面码作为拓扑量子存储器的性质及其解码机制。自那时起，表面码因其优越的性能和对实验实现的友好性，吸引了大量的理论和实验研究，包括对其容错阈值的精确计算、逻辑门操作方案的优化以及在各种物理系统中的实验验证。

核心原理

结构与编码

表面码（或其变体环面码）的局部示意图。图中物理量子比特（自旋）位于晶格的边上。高亮显示了一个顶点（vertex）稳定子（涉及四个$X$算符）和一个面元（plaquette）稳定子（涉及四个$Z$算符）。

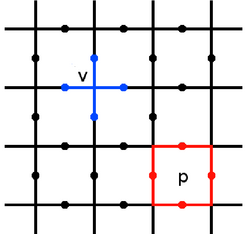
表面码通常定义在一个二维的量子比特晶格上，例如方格（或旋转方格）排列。物理量子比特可以放置在晶格的边（英語：edge）上（如基塔耶夫最初提出的模型），也可以放置在顶点（英語：vertex）或面（英語：face/plaquette）上（在一些变体或对偶表示中）。最常见的构造是将物理量子比特置于晶格的边上。逻辑量子比特的信息则非局域地编码在这些物理量子比特的集体状态中。

一个码距为 $d$ 的表面码，通常需要 ${\mathcal {O}}(d^{2})$ 个物理量子比特来编码一个或两个逻辑量子比特（取决于边界条件和具体设计）。码距 $d$ 与晶格的尺寸相关，它决定了编码能够检测和纠正的错误的数量。具体而言，一个码距为 $d$ 的码可以检测最多 $d-1$ 个任意单物理量子比特错误，并纠正最多 $t=\lfloor (d-1)/2\rfloor$ 个此类错误。

稳定子算符

表面码是一种稳定子码，其编码空间（英語：codespace，即逻辑量子比特的有效希尔伯特空间）被定义为一组称为稳定子生成元（英語：stabilizer generators）的厄米算符的共同 $+1$ 本征空间。这些稳定子生成元由局域的泡利算符张量积构成，即每个生成元仅作用于晶格上少数几个（通常是几何上邻近的）物理量子比特。

在一个标准的、物理量子比特位于边的表面码中，主要有两种类型的稳定子算符：

• 顶点算符（英語：Vertex Operators），也常称为星算符（英語：Star Operators）：对于晶格中的每一个顶点 $s$（不包括某些边界上的顶点），关联一个顶点算符 $A_{s}$ (或 $S_{s}$)。该算符定义为作用在所有以该顶点 $s$ 为端点的边上的物理量子比特的泡利$X$算符的张量积：

$A_{s}=\prod _{i\in {\text{star}}(s)}X_{i}$

其中 ${\text{star}}(s)$ 表示以顶点 $s$ 为公共端点的边的集合，$X_{i}$ 是作用于第 $i$ 个量子比特（边 $i$）的泡利$X$算符。

• 面算符（英語：Plaquette Operators），也常称为方格算符：对于晶格中的每一个面（或方格单元） $p$，关联一个面算符 $B_{p}$。该算符定义为作用在构成该面 $p$ 边界的所有边上的物理量子比特的泡利$Z$ 算符的张量积：

$B_{p}=\prod _{j\in {\text{boundary}}(p)}Z_{j}$

其中 ${\text{boundary}}(p)$ 表示构成面 $p$ 边界的边的集合，$Z_{j}$ 是作用于第 $j$ 个量子比特（边 $j$）的泡利$Z$算符。

所有这些顶点算符和面算符相互对易（$[A_{s},A_{s'}]=0$, $[B_{p},B_{p'}]=0$, $[A_{s},B_{p}]=0$），并且它们的平方均为单位算符（$A_{s}^{2}=I$, $B_{p}^{2}=I$）。逻辑上编码的量子态 $|\psi _{L}\rangle$ 必须满足对于所有的 $s$ 和 $p$，$A_{s}|\psi _{L}\rangle =|\psi _{L}\rangle$ 且 $B_{p}|\psi _{L}\rangle =|\psi _{L}\rangle$。

错误检测与综合征

当物理量子比特发生错误时（例如，由于退相干或不完美的门操作），编码态可能会偏离 $+1$ 本征空间。通过周期性地测量所有稳定子生成元 $A_{s}$ 和 $B_{p}$ 的本征值，可以检测到错误的发生。如果某个稳定子算符的测量结果为 $-1$（而不是预期的 $+1$），则表明在其作用范围内的物理量子比特上发生了与其反对易的错误。例如，一个 $Z$ 错误作用在一个与顶点 $s$ 相连的边上，会使得 $A_{s}$ 的测量值从 $+1$ 翻转到 $-1$。类似地，一个 $X$ 错误作用在一个构成面 $p$ 边界的边上，会使得 $B_{p}$ 的测量值翻转。

所有稳定子测量的结果构成一个错误综合征（英語：error syndrome）。这个综合征给出了关于错误类型及其位置（或更准确地说，错误链的端点）的信息，但重要的是，它并不泄露编码的逻辑量子信息本身。

逻辑算符

逻辑量子比特的信息由非局域的、跨越整个晶格的“弦”状（英語：string-like）算符来表示和操作。这些逻辑算符（英語：Logical Operators）必须与所有的稳定子算符（$A_{s}$ 和 $B_{p}$）对易，以确保它们不会将编码态移出码空间或改变稳定子测量结果。然而，逻辑算符对之间（例如逻辑${\bar {X}}$和逻辑${\bar {Z}}$）则需要满足与单量子比特泡利算符相似的代数关系（例如，逻辑${\bar {X}}$和逻辑${\bar {Z}}$应该反对易）。

对于一个在具有合适边界（例如，某些边界是“粗糙”的，某些是“平滑”的）的平面上编码单个逻辑量子比特的表面码：

• 逻辑${\bar {Z}}$算符（$Z_{L}$）可以是一条连接晶格两个相对“类型”的边界（例如，从一个“粗糙”边界到另一个“粗糙”边界）的泡利$Z$算符链。
• 逻辑${\bar {X}}$算符（$X_{L}$）则可以是一条类似地连接另外两个相对“类型”的边界（例如，从一个“平滑”边界到另一个“平滑”边界，通常在对偶格上或垂直方向上）的泡利$X$算符链。

这些算符的非局域性是拓扑保护的关键：一个局域错误（作用于少数物理量子比特）不太可能同时改变一个完整的逻辑算符链从而导致逻辑错误。只有当错误链也连接了相同的两个边界时，才会发生逻辑错误。码距 $d$ 可以看作是形成这样一个最短的、非平凡的逻辑算符链（或等效的错误链）所包含的物理量子比特数。

容错特性

容错阈值

表面码的一个显著优势是其相对较高的容错阈值（英語：fault-tolerance threshold）。这意味着只要物理量子比特的错误率（包括门操作错误、测量错误和存储错误）低于某个特定的阈值 $p_{th}$，就可以通过增加码距 $d$（即增大晶格尺寸）来任意降低逻辑错误率 $p_{L}$。即使仅依赖于物理量子比特之间的最近邻相互作用，表面码也能达到较高的阈值。

对于标准的电路级噪声模型，表面码的阈值估计值通常在 $0.5\%$ 到 $1.1\%$ 之间。具体阈值的大小依赖于诸多因素，如特定的噪声模型（例如，错误是独立同分布的，还是存在关联，或是偏置噪声）、所采用的解码器算法以及量子电路（特别是综合征提取电路）的具体实现细节。在存在偏置噪声（例如，$Z$错误远多于$X$或$Y$错误）的情况下，特定设计的表面码变体（如XZZX码）可以展现出更高的阈值。

近期的实验进展显著，例如已有研究在超导量子计算平台上成功运行了码距达到7的表面码，并观察到了逻辑错误率随码距增加而下降的趋势，且其性能表现已接近或低于理论预测的容错阈值要求。

解码

从测得的错误综合征推断出最可能发生的物理错误（或等效的错误链），并确定相应的校正操作（通常是应用泡利算符）的过程称为解码（英語：decoding）。解码器的效率和准确性对表面码的整体性能至关重要。

由于表面码的错误检测可以映射到二维或三维（如果考虑时间上的错误传播）的匹配问题，最小权完美匹配（英語：Minimum Weight Perfect Matching, MWPM）算法是表面码（特别是对于独立错误模型）最常用且非常有效的解码器之一。MWPM算法试图找到一组连接所有非平凡综合征测量结果（$-1$稳定子）的“弦”，使得这些弦的总“权重”（通常与错误的概率相关）最小。

其他解码算法包括基于置信传播（英語：Belief Propagation）的解码器、基于机器学习的解码器、以及专门针对特定噪声模型（如偏置噪声或关联错误）优化的解码器。解码器的选择和优化是表面码研究中的一个活跃领域。

主要变体

为了优化性能、降低资源开销或适应特定硬件特性，已提出多种表面码的变体：

• 旋转表面码（英語：Rotated Surface Code）：通过将标准方格晶格旋转45度进行布局，可以在保持相同码距（纠错能力）的前提下，将所需的物理量子比特数量减少大约一半。这对于在物理量子比特资源有限的近期设备上实现具有重要意义，并且是当前实验中最常采用的表面码形式。

• XZZX表面码 / XY表面码：这些是表面码的变体，其稳定子定义与标准表面码不同。例如，XZZX表面码使用形如 $XZZX$ 的混合泡利算符作为其面算符（或顶点算符，取决于具体构造），而XY表面码则可能在其稳定子中包含 $Y$ 算符。这类变体的设计目标之一是更好地适应具有偏置噪声（英語：biased noise）特性的物理系统，即系统中某一类型的错误（例如相位错误，即$Z$错误）远比其他类型的错误（例如比特翻转错误，即$X$错误）更为频繁。在这样的偏置噪声环境下，这些变体可以展现出比标准表面码更高的有效容错阈值或更低的逻辑错误率。

逻辑门操作

在编码的逻辑量子比特上执行计算操作是容错量子计算的关键。表面码支持一套通用的逻辑门操作，但不同类型的门实现方式和资源开销有所不同。

• 克利福德门（英語：Clifford gates）：包括Hadamard门（H）、S门（相位门）、CNOT门、CZ门等。在表面码中，许多克利福德门可以通过编码形变（英語：Code Deformation，也称辫操作或缺陷编织）或晶格手术（英語：Lattice Surgery）等技术相对高效地实现。晶格手术是一种强大的技术，它通过合并（英語：merging）和分割（英語：splitting）不同的表面码片元（英語：patches）来执行逻辑门。例如，通过特定方式合并和分割两个分别编码逻辑量子比特的表面码片元，可以实现逻辑CNOT门。这些操作通常可以保持容错性，即操作过程中发生的物理错误也可以被检测和纠正。

• 非克利福德门（例如T门）：通用的量子计算要求至少一个非克利福德门（如T门或CCZ门）来构成完备门集。然而，根据Eastin-Knill定理，任何量子纠错码都不可能拥有一整套通用的、横向实现（英語：transversal）的容错逻辑门。在表面码中，非克利福德门通常不能直接通过简单的编码形变或晶格手术容错地实现。

实现非克利福德逻辑门（最典型的是T门）通常依赖于一种名为魔术态蒸馏（英語：Magic State Distillation）的资源密集型协议。魔法态蒸馏过程利用大量的克利福德操作和测量，从多个带有噪声的“魔术态”（例如 $T$ 门的本征态 $|T\rangle =(|0\rangle +e^{i\pi /4}|1\rangle )/{\sqrt {2}}$）副本中，概率性地提纯出少量高保真度的魔术态。随后，这些高保真度的魔法态可以通过门隐形传态（英語：gate teleportation）的方式与克利福德操作结合，间接实现非克利福德逻辑门，如 $T$ 门。由于魔法态蒸馏对物理量子比特和操作时间均有巨大开销，优化其效率是降低容错量子计算整体资源需求的关键研究方向。

• 逻辑测量：逻辑量子比特的测量可以通过测量构成相应逻辑泡利算符（如$Z_{L}$或$X_{L}$）的所有物理量子比特来完成。测量结果需要进行解码以排除测量过程中可能发生的错误。

优势与挑战

优势

• 高容错阈值：如前所述，表面码拥有目前已知最高的容错阈值之一（约$1\%$），这意味着对物理量子比特的质量要求相对宽松。
• 二维局域性：稳定子和逻辑门操作（特别是通过晶格手术）仅需物理量子比特之间的最近邻相互作用。这与许多固态量子计算平台（如超导量子比特、量子点）的物理约束非常吻合。
• 相对简单的结构：其规则的二维晶格结构易于设计和扩展。
• 成熟的解码算法：存在如MWPM这样高效且性能良好的解码算法。

挑战

• 较低的编码率：逻辑量子比特数量 $k$ 相对于物理量子比特数量 $n$ 的比率 $k/n$ 较低。对于码距为 $d$ 的标准表面码，通常需要 $n\approx {\mathcal {O}}(d^{2})$ 个物理量子比特来编码 $k=1$ 或 $k=2$ 个逻辑量子比特。这意味着为了实现高精度的逻辑量子比特（需要较大的 $d$），需要大量的物理量子比特。
• 非克利福德门的高昂代价：如前所述，实现非克利福德逻辑门所需的魔法态蒸馏过程资源消耗巨大，这构成了构建通用容错量子计算机的主要开销之一，可能占据整个计算资源需求的绝大部分。
• 连接性与布局：虽然二维局域性是优点，但在大规模系统中，如何有效地连接和控制数百万甚至更多的物理量子比特，同时保持低错误率和高连通性，仍然是一个巨大的工程挑战。
• 解码速度：虽然MWPM等算法在理论上有效，但在大规模、高速运行的量子计算机中，解码器必须能够实时处理综合征信息并快速给出校正指令，这对解码器的计算速度提出了极高要求。

尽管存在这些挑战，表面码凭借其稳健性、较高的容错阈值以及对现有和近期硬件平台的适应性，在当前的容错量子计算研究和实验进展中仍占据核心地位，并被广泛认为是实现首个大规模容错量子计算机的最有希望的路径。

参见

• 量子纠错
• 稳定子码
• 环面码 (Toric Code)
• 颜色码 (Color Code)
• 拓扑量子计算
• 容错量子计算
• 量子阈值定理
• 阿列克谢·基塔耶夫