表面碼

表面碼（英語：Surface Code）是一種重要且極具前景的量子糾錯碼（QECC），屬於穩定子碼和拓撲量子糾錯碼（英語：topological quantum error correction code）的範疇。表面碼因其具有較高的容錯閾值、僅需最近鄰相互作用以及對實際量子計算機硬件平台（特別是二維布局的量子比特陣列）的良好適應性而受到廣泛研究。其核心思想是將邏輯量子比特的信息編碼到分布於二維平面（「表面」）上的大量物理量子比特中，並通過測量局域的穩定子算符來檢測和糾正發生的錯誤。這種編碼方式使得邏輯信息受到拓撲性質的保護，對局域物理錯誤具有天然的魯棒性。表面碼被普遍認為是構建大規模容錯量子計算機最有希望的候選方案之一。

歷史與發展

表面碼的概念起源於阿列克謝·基塔耶夫（Alexei Kitaev）在1997年提出的環面碼（英語：Toric Code），這是一種在具有周期性邊界條件（環面拓撲）的二維晶格上定義的拓撲量子糾錯碼。隨後，謝爾蓋·布拉維伊（Sergey Bravyi）和基塔耶夫於1998年研究了具有開放邊界（平面）的晶格，從而發展出嚴格意義上的表面碼。埃里克·丹尼斯（Eric Dennis）、基塔耶夫、安德魯·蘭達爾（Andrew Landahl）和約翰·普雷斯基爾（John Preskill）在2001年進一步闡述了表面碼作為拓撲量子存儲器的性質及其解碼機制。自那時起，表面碼因其優越的性能和對實驗實現的友好性，吸引了大量的理論和實驗研究，包括對其容錯閾值的精確計算、邏輯門操作方案的優化以及在各種物理系統中的實驗驗證。

核心原理

結構與編碼

表面碼（或其變體環面碼）的局部示意圖。圖中物理量子比特（自旋）位於晶格的邊上。高亮顯示了一個頂點（vertex）穩定子（涉及四個$X$算符）和一個面元（plaquette）穩定子（涉及四個$Z$算符）。

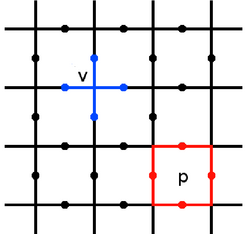
表面碼通常定義在一個二維的量子比特晶格上，例如方格（或旋轉方格）排列。物理量子比特可以放置在晶格的邊（英語：edge）上（如基塔耶夫最初提出的模型），也可以放置在頂點（英語：vertex）或面（英語：face/plaquette）上（在一些變體或對偶表示中）。最常見的構造是將物理量子比特置於晶格的邊上。邏輯量子比特的信息則非局域地編碼在這些物理量子比特的集體狀態中。

一個碼距為 $d$ 的表面碼，通常需要 ${\mathcal {O}}(d^{2})$ 個物理量子比特來編碼一個或兩個邏輯量子比特（取決於邊界條件和具體設計）。碼距 $d$ 與晶格的尺寸相關，它決定了編碼能夠檢測和糾正的錯誤的數量。具體而言，一個碼距為 $d$ 的碼可以檢測最多 $d-1$ 個任意單物理量子比特錯誤，並糾正最多 $t=\lfloor (d-1)/2\rfloor$ 個此類錯誤。

穩定子算符

表面碼是一種穩定子碼，其編碼空間（英語：codespace，即邏輯量子比特的有效希爾伯特空間）被定義為一組稱為穩定子生成元（英語：stabilizer generators）的厄米算符的共同 $+1$ 本徵空間。這些穩定子生成元由局域的泡利算符張量積構成，即每個生成元僅作用於晶格上少數幾個（通常是幾何上鄰近的）物理量子比特。

在一個標準的、物理量子比特位於邊的表面碼中，主要有兩種類型的穩定子算符：

• 頂點算符（英語：Vertex Operators），也常稱為星算符（英語：Star Operators）：對於晶格中的每一個頂點 $s$（不包括某些邊界上的頂點），關聯一個頂點算符 $A_{s}$ (或 $S_{s}$)。該算符定義為作用在所有以該頂點 $s$ 為端點的邊上的物理量子比特的泡利$X$算符的張量積：

$A_{s}=\prod _{i\in {\text{star}}(s)}X_{i}$

其中 ${\text{star}}(s)$ 表示以頂點 $s$ 為公共端點的邊的集合，$X_{i}$ 是作用於第 $i$ 個量子比特（邊 $i$）的泡利$X$算符。

• 面算符（英語：Plaquette Operators），也常稱為方格算符：對於晶格中的每一個面（或方格單元） $p$，關聯一個面算符 $B_{p}$。該算符定義為作用在構成該面 $p$ 邊界的所有邊上的物理量子比特的泡利$Z$ 算符的張量積：

$B_{p}=\prod _{j\in {\text{boundary}}(p)}Z_{j}$

其中 ${\text{boundary}}(p)$ 表示構成面 $p$ 邊界的邊的集合，$Z_{j}$ 是作用於第 $j$ 個量子比特（邊 $j$）的泡利$Z$算符。

所有這些頂點算符和面算符相互對易（$[A_{s},A_{s'}]=0$, $[B_{p},B_{p'}]=0$, $[A_{s},B_{p}]=0$），並且它們的平方均為單位算符（$A_{s}^{2}=I$, $B_{p}^{2}=I$）。邏輯上編碼的量子態 $|\psi _{L}\rangle$ 必須滿足對於所有的 $s$ 和 $p$，$A_{s}|\psi _{L}\rangle =|\psi _{L}\rangle$ 且 $B_{p}|\psi _{L}\rangle =|\psi _{L}\rangle$。

錯誤檢測與綜合徵

當物理量子比特發生錯誤時（例如，由於退相干或不完美的門操作），編碼態可能會偏離 $+1$ 本徵空間。通過周期性地測量所有穩定子生成元 $A_{s}$ 和 $B_{p}$ 的本徵值，可以檢測到錯誤的發生。如果某個穩定子算符的測量結果為 $-1$（而不是預期的 $+1$），則表明在其作用範圍內的物理量子比特上發生了與其反對易的錯誤。例如，一個 $Z$ 錯誤作用在一個與頂點 $s$ 相連的邊上，會使得 $A_{s}$ 的測量值從 $+1$ 翻轉到 $-1$。類似地，一個 $X$ 錯誤作用在一個構成面 $p$ 邊界的邊上，會使得 $B_{p}$ 的測量值翻轉。

所有穩定子測量的結果構成一個錯誤綜合徵（英語：error syndrome）。這個綜合徵給出了關於錯誤類型及其位置（或更準確地說，錯誤鏈的端點）的信息，但重要的是，它並不泄露編碼的邏輯量子信息本身。

邏輯算符

邏輯量子比特的信息由非局域的、跨越整個晶格的「弦」狀（英語：string-like）算符來表示和操作。這些邏輯算符（英語：Logical Operators）必須與所有的穩定子算符（$A_{s}$ 和 $B_{p}$）對易，以確保它們不會將編碼態移出碼空間或改變穩定子測量結果。然而，邏輯算符對之間（例如邏輯 ${\bar {X}}$ 和邏輯 ${\bar {Z}}$ ）則需要滿足與單量子比特泡利算符相似的代數關係（例如，邏輯 ${\bar {X}}$ 和邏輯 ${\bar {Z}}$ 應該反對易）。

對於一個在具有合適邊界（例如，某些邊界是「粗糙」的，某些是「平滑」的）的平面上編碼單個邏輯量子比特的表面碼：

• 邏輯 ${\bar {Z}}$ 算符（$Z_{L}$）可以是一條連接晶格兩個相對「類型」的邊界（例如，從一個「粗糙」邊界到另一個「粗糙」邊界）的泡利$Z$ 算符鏈。
• 邏輯 ${\bar {X}}$ 算符（$X_{L}$）則可以是一條類似地連接另外兩個相對「類型」的邊界（例如，從一個「平滑」邊界到另一個「平滑」邊界，通常在對偶格上或垂直方向上）的泡利 $X$ 算符鏈。

這些算符的非局域性是拓撲保護的關鍵：一個局域錯誤（作用於少數物理量子比特）不太可能同時改變一個完整的邏輯算符鏈從而導致邏輯錯誤。只有當錯誤鏈也連接了相同的兩個邊界時，才會發生邏輯錯誤。碼距 $d$ 可以看作是形成這樣一個最短的、非平凡的邏輯算符鏈（或等效的錯誤鏈）所包含的物理量子比特數。

容錯特性

容錯閾值

表面碼的一個顯著優勢是其相對較高的容錯閾值（英語：fault-tolerance threshold）。這意味着只要物理量子比特的錯誤率（包括門操作錯誤、測量錯誤和存儲錯誤）低於某個特定的閾值 $p_{th}$，就可以通過增加碼距 $d$（即增大晶格尺寸）來任意降低邏輯錯誤率 $p_{L}$。即使僅依賴於物理量子比特之間的最近鄰相互作用，表面碼也能達到較高的閾值。

對於標準的電路級噪聲模型，表面碼的閾值估計值通常在 $0.5\%$ 到 $1.1\%$ 之間。具體閾值的大小依賴於諸多因素，如特定的噪聲模型（例如，錯誤是獨立同分布的，還是存在關聯，或是偏置噪聲）、所採用的解碼器算法以及量子電路（特別是綜合徵提取電路）的具體實現細節。在存在偏置噪聲（例如，$Z$ 錯誤遠多於 $X$ 或 $Y$ 錯誤）的情況下，特定設計的表面碼變體（如XZZX碼）可以展現出更高的閾值。

近期的實驗進展顯著，例如已有研究在超導量子計算平台上成功運行了碼距達到7的表面碼，並觀察到了邏輯錯誤率隨碼距增加而下降的趨勢，且其性能表現已接近或低於理論預測的容錯閾值要求。

解碼

從測得的錯誤綜合徵推斷出最可能發生的物理錯誤（或等效的錯誤鏈），並確定相應的校正操作（通常是應用泡利算符）的過程稱為解碼（英語：decoding）。解碼器的效率和準確性對表面碼的整體性能至關重要。

由於表面碼的錯誤檢測可以映射到二維或三維（如果考慮時間上的錯誤傳播）的匹配問題，最小權完美匹配（英語：Minimum Weight Perfect Matching, MWPM）算法是表面碼（特別是對於獨立錯誤模型）最常用且非常有效的解碼器之一。MWPM算法試圖找到一組連接所有非平凡綜合徵測量結果（$-1$穩定子）的「弦」，使得這些弦的總「權重」（通常與錯誤的概率相關）最小。

其他解碼算法包括基於置信傳播（英語：Belief Propagation）的解碼器、基於機器學習的解碼器、以及專門針對特定噪聲模型（如偏置噪聲或關聯錯誤）優化的解碼器。解碼器的選擇和優化是表面碼研究中的一個活躍領域。

主要變體

為了優化性能、降低資源開銷或適應特定硬件特性，已提出多種表面碼的變體：

旋轉表面碼（英語：Rotated Surface Code）

通過將標準方格晶格旋轉45度進行布局，可以在保持相同碼距（糾錯能力）的前提下，將所需的物理量子比特數量減少大約一半。這對於在物理量子比特資源有限的近期設備上實現具有重要意義，並且是當前實驗中最常採用的表面碼形式。

XZZX表面碼 / XY表面碼

這些是表面碼的變體，其穩定子定義與標準表面碼不同。例如，XZZX表面碼使用形如 $XZZX$ 的混合泡利算符作為其面算符（或頂點算符，取決於具體構造），而XY表面碼則可能在其穩定子中包含 $Y$ 算符。這類變體的設計目標之一是更好地適應具有偏置噪聲（英語：biased noise）特性的物理系統，即系統中某一類型的錯誤（例如相位錯誤，即$Z$錯誤）遠比其他類型的錯誤（例如比特翻轉錯誤，即$X$錯誤）更為頻繁。在這樣的偏置噪聲環境下，這些變體可以展現出比標準表面碼更高的有效容錯閾值或更低的邏輯錯誤率。

邏輯門操作

在編碼的邏輯量子比特上執行計算操作是容錯量子計算的關鍵。表面碼支持一套通用的邏輯門操作，但不同類型的門實現方式和資源開銷有所不同。

克利福德門（英語：Clifford gates）

包括Hadamard門（H）、S門（相位門）、CNOT門、CZ門等。在表面碼中，許多克利福德門可以通過編碼形變（英語：Code Deformation，也稱辮操作或缺陷編織）或晶格手術（英語：Lattice Surgery）等技術相對高效地實現。晶格手術是一種強大的技術，它通過合併（英語：merging）和分割（英語：splitting）不同的表面碼片元（英語：patches）來執行邏輯門。例如，通過特定方式合併和分割兩個分別編碼邏輯量子比特的表面碼片元，可以實現邏輯CNOT門。這些操作通常可以保持容錯性，即操作過程中發生的物理錯誤也可以被檢測和糾正。

非克利福德門（例如T門）

通用的量子計算要求至少一個非克利福德門（如T門或CCZ門）來構成完備門集。然而，根據Eastin-Knill定理，任何量子糾錯碼都不可能擁有一整套通用的、橫向實現（英語：transversal）的容錯邏輯門。在表面碼中，非克利福德門通常不能直接通過簡單的編碼形變或晶格手術容錯地實現。

實現非克利福德邏輯門（最典型的是T門）通常依賴於一種名為魔術態蒸餾（英語：Magic State Distillation）的資源密集型協議。魔法態蒸餾過程利用大量的克利福德操作和測量，從多個帶有噪聲的「魔術態」（例如 $T$ 門的本徵態 $|T\rangle =(|0\rangle +e^{i\pi /4}|1\rangle )/{\sqrt {2}}$）副本中，概率性地提純出少量高保真度的魔術態。隨後，這些高保真度的魔法態可以通過門隱形傳態（英語：gate teleportation）的方式與克利福德操作結合，間接實現非克利福德邏輯門，如 $T$ 門。由於魔法態蒸餾對物理量子比特和操作時間均有巨大開銷，優化其效率是降低容錯量子計算整體資源需求的關鍵研究方向。

邏輯測量

邏輯量子比特的測量可以通過測量構成相應邏輯泡利算符（如$Z_{L}$或$X_{L}$）的所有物理量子比特來完成。測量結果需要進行解碼以排除測量過程中可能發生的錯誤。

優勢與挑戰

表面碼的核心優勢在於其相對較高的物理錯誤容錯閾值，通常在0.1%至1%之間 ，這主要源於其二維平面結構中穩定子的局部性 ，從而對物理量子比特的質量要求更為寬鬆。此特性與二維局部架構的天然兼容性相輔相成，表面碼僅需近鄰相互作用即可進行穩定子測量 ，完美契合超導量子比特和離子阱等主流硬件平台的固有架構，進而簡化了器件設計並被Google、中國科學技術大學等團隊採用。加之其受益於如最小權完美匹配（MWPM）等相對簡單且高效成熟的解碼算法，這些算法能利用錯誤的幾何特性，在實踐中表現接近最優並已實現實時解碼。

然而，表面碼的廣泛應用也面臨若干重大挑戰。最為顯著的是其巨大的量子比特開銷，編碼單個邏輯量子比特往往需數百至數千個物理量子比特 ，例如在0.1%物理錯誤率下，可能需要1000至10000個物理量子比特。其編碼率隨碼距 $d$ 以約 $1/d^{2}$ 的速度下降 ，構建大規模量子計算機需要相當大的資源消耗。另一項關鍵挑戰在於表面碼對特定的關聯錯誤較為敏感。儘管它對獨立的泡利錯誤具有良好魯棒性，但在面對空間或時間上存在統計相關性的錯誤時，其性能可能顯著下降 。某些關聯錯誤模式甚至可能「災難性地」影響邏輯錯誤率的指數級抑制，導致邏輯錯誤率不再隨碼距增加而改善，形成「本底噪聲」 。此外，表面碼上邏輯門操作的複雜性與資源成本也不容忽視。雖然克利福德門可通過晶格手術等技術實現，但對於通用量子計算至關重要的非克利福德門（如T門），通常依賴於資源高度密集型的魔態蒸餾過程。這會消耗大量額外的物理量子比特和操作時間，其開銷甚至可能主導整個算法的資源需求，是實現可擴展量子計算必須解決的關鍵問題。

參見

• 量子糾錯
• 穩定子碼
• 環面碼（Toric Code）
• 顏色碼（Color Code）
• 拓撲量子計算
• 容錯量子計算
• 量子閾值定理
• 阿列克謝·基塔耶夫