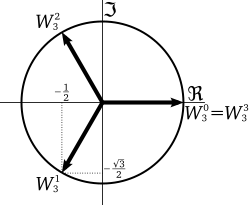
 复平面上的三次单位根
复平面上的三次单位根
数学上, 次单位根是
次单位根是 次幂为1的复数。它们位于复平面的单位圆上,构成正多边形的顶点,但最多只可有两个顶点同时标在实数线上。
次幂为1的复数。它们位于复平面的单位圆上,构成正多边形的顶点,但最多只可有两个顶点同时标在实数线上。

这方程的复数根  为
为 次单位根。
次单位根。
单位的  次根有
次根有  个:
个:
 。
。
单位的  次根以乘法构成
次根以乘法构成 阶循环群。它的生成元是
阶循环群。它的生成元是  次本原单位根。
次本原单位根。 次本原单位根是
次本原单位根是 ,其中
,其中 和
和 互质。
互质。 次本原单位根数目为欧拉函数
次本原单位根数目为欧拉函数 。
全体i次单位根对普通乘法作成群,即i次单位根群。所有全体i次单位根群在普通乘法下也可作成群,且这是一个无限交换群,这个无限交换群里的每个元素的阶都有限。
。
全体i次单位根对普通乘法作成群,即i次单位根群。所有全体i次单位根群在普通乘法下也可作成群,且这是一个无限交换群,这个无限交换群里的每个元素的阶都有限。
一次单位根有一个:  。
。
二次单位根有两个:  和
和 ,只有
,只有 是本原根。
是本原根。
三次单位根是

其中 是虚数单位;除
是虚数单位;除 外都是本原根。
外都是本原根。
四次单位根是

其中 和
和 是本原根。
是本原根。
当 不小于
不小于 时,
时, 次单位根总和为
次单位根总和为 。这一结果可以用不同的方法证明。一个基本方法是等比级数:
。这一结果可以用不同的方法证明。一个基本方法是等比级数:
 。
。
第二个证法是它们在复平面上构成正多边形的顶点,而从对称性知这多边形的重心在原点。
还有一个证法利用关于方程根与系数的韦达定理,由分圆方程的 项系数为零得出。
项系数为零得出。





















