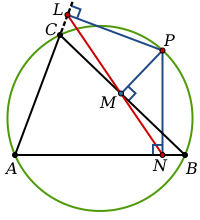
 三角形 ABC 為黑色,從 P 延伸出去的三條垂線為藍色,由此得到的垂足三角形 LMN 為紅色
三角形 ABC 為黑色,從 P 延伸出去的三條垂線為藍色,由此得到的垂足三角形 LMN 為紅色
在幾何學上,垂足三角形(英語:Pedal triangle)是將一個點投影至三角形的邊上所得到的三角形。
具體地說,考慮一個三角形 ,選定一個異於頂點
,選定一個異於頂點 的點
的點 。通過
。通過 對三角形的三邊做垂直線,將這些垂直線與
對三角形的三邊做垂直線,將這些垂直線與 的交點分別命名為
的交點分別命名為 ,則三角形
,則三角形 是一個垂足三角形。
是一個垂足三角形。
如果 不是鈍角三角形,則其垂足三角形
不是鈍角三角形,則其垂足三角形 的內角角度分別為
的內角角度分別為 、
、 、
、 。[1]
若
。[1]
若 點位於三角形
點位於三角形 的特殊中心上,則有一些特殊情況:
的特殊中心上,則有一些特殊情況:
- 若
 是
是 的垂心,則
的垂心,則 是垂心三角形(英語:Orthic triangle)。
是垂心三角形(英語:Orthic triangle)。
- 若
 是
是 的內心,則
的內心,則 是
是 之內切圓的三個切點。
之內切圓的三個切點。
- 若
 是
是 的外心,則
的外心,則 是中點三角形。
是中點三角形。
若 點以三角形
點以三角形 為基準的三線坐標是
為基準的三線坐標是 ,則其垂足三角形的頂點
,則其垂足三角形的頂點 坐標為:
坐標為:



 P 在外接圓上的情形,此時垂足三角形退化為一條線(紅色)
P 在外接圓上的情形,此時垂足三角形退化為一條線(紅色)
 卡諾定理:紅色區域與藍色區域的面積相等
卡諾定理:紅色區域與藍色區域的面積相等
若 點位於
點位於 的外接圓上,則
的外接圓上,則 共線,反之亦然。這條線被稱為垂足線(英語:Pedal line),又稱為西姆松線(英語:Simson line)。
共線,反之亦然。這條線被稱為垂足線(英語:Pedal line),又稱為西姆松線(英語:Simson line)。
 六點滿足以下等式:[2]
六點滿足以下等式:[2]

 三角形 ABC 為紅色,從 P 延伸至頂點的三條線為藍色,由此得到的反垂足三角形 LMN 為黑色
三角形 ABC 為紅色,從 P 延伸至頂點的三條線為藍色,由此得到的反垂足三角形 LMN 為黑色
過 作一條垂直於
作一條垂直於 的直線,過
的直線,過 作一條垂直於
作一條垂直於 的直線,過
的直線,過 作一條垂直於
作一條垂直於 的直線,則這三條直線構成的三角形稱為反垂足三角形(英語:Antipedal triangle)。在這個反垂足三角形中,設與
的直線,則這三條直線構成的三角形稱為反垂足三角形(英語:Antipedal triangle)。在這個反垂足三角形中,設與 相對的頂點為
相對的頂點為 ,與
,與 相對的頂點為
相對的頂點為 ,與
,與 相對的頂點為
相對的頂點為 。
。
 是
是 在
在 點上的垂足三角形,這也是其名稱的由來。
點上的垂足三角形,這也是其名稱的由來。
若 點以三角形
點以三角形 為基準的三線坐標是
為基準的三線坐標是 ,則反垂足三角形的頂點
,則反垂足三角形的頂點 坐標為:[3]
坐標為:[3]



一個特殊的例子是,如果 點位於內心,則該反垂足三角形以
點位於內心,則該反垂足三角形以 的三個旁心為頂點。
的三個旁心為頂點。

































