二十面体

二十面體

部分的二十面體 正二十面體 正九角反稜柱 正三角台塔反角柱 同相雙三角台塔柱 大二十面體 完全星形二十面體
定義	由20個面組成的多面體
共同性質
面	20

在幾何學中，二十面體（icosahedron）是指具有二十個面的多面體。在三維歐幾里得空間中有兩種二十面體屬於正多面體，分別為凸正二十面體和大二十面體。一般俗稱的「二十面體」通常代表前者（凸正二十面體）。 除此之外，亦有許多二十面體是等面或等角的，例如十方偏方面體（等面），也有的二十面體所有的面都是正多邊形，例如正十八角柱、九角反稜柱、正三角台塔反角柱、同相和異相雙三角帳塔柱等。也有些二十面體是半正多面體，例如正十八角柱和正九角反稜柱。此外，亦有部分二十面體是稀有多面體，例如完全星形二十面體及稀有九角星二十面體等。

不同種類的二十面體有不同用途。例如凸均勻二十面體可以被製作為骰子；部分的二十面體結構會出現在一些晶體結構、化學物質或生物體結構中。具有张拉整体結構的二十面體則可以用於兒童玩具的設計、封裝太空設備用於探索其他行星時的著陸的機器人等。

正二十面體

凸正二十面體

大二十面體

兩種正二十面體

所有三維歐幾里得空間的二十面體中，有兩種多面體屬於正多面體。一種為凸多面體，另一種為非凸多面體。這兩種立體都具有30條邊和20個三角形面，且這兩種立體的12個頂點都是5個三角形的公共頂點，並且皆具有二十面體群對稱性。詞彙「正二十面體」通常表達的是凸的正二十面體，而非凸的正二十面體稱為大二十面體。

凸正二十面體

二十面的骰子

主条目：正二十面體

凸正二十面體通常簡稱為正二十面體，在特定領域中簡稱為二十面體，是五個柏拉圖立體之一，其在施萊夫利符號中可以用{3, 5}來表示，共有20個正三角形面，且每個頂點都是5個正三角形的公共頂點，並且這些面在頂點周圍以正五邊形之邊的排列方式進行排列，換言之即凸正二十面體的頂點圖為正五邊形。

凸正二十面體的對偶多面體是凸正十二面體，用施萊夫利符號表示為{5, 3}。其包含了12個正五邊形面，每個頂點都是3個正五邊形的公共頂點。

這種二十面體的特別之處在於——有不少多面體是基於這種立體建構的，其中一個顯著的例子是星形二十面體，這些立體共有59種（星形的僅58種，另外一個是正二十面體本身）。這些星形多面體皆可透過米勒的規則、以正二十面體作為核建構而來。此外的例子還有詹森多面體，許多詹森多面體可透過移除正二十面體的局部結構（如移除五角錐）來構建。

由於其等面的特性，因此其非常適合製成骰子。

大二十面體

大二十面體的立體模型

主条目：大二十面體

大二十面體是四個克卜勒－龐索立體之一，其在施萊夫利符號中可以用{3, 5/2}來表示，與凸的正二十面體有相同的面數、邊數和頂點數，差別在於頂點圖的不同：大二十面體的頂點圖是五角星而非五邊形，導致其成為自相交的多面體。

大二十面體的對偶多面體為大星形十二面體，施萊夫利符號記為{5/2, 3}，其包含了12個正五角星面，每個頂點都是3個正五角星的公共頂點。

星形二十面體

主条目：星形二十面體

多面體的星形化是指把多面體的面和邊沿伸直到向外相交成星形的立體。這個過程是對稱地完成的，以便生成保留了與原像相同的整體對稱性。

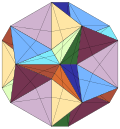
在書籍《五十九種二十面體》，考克斯特等人列出了58種正二十面體的星形化體。其中，許多星形二十面體的組成面都是單一面（即沒有同一個面包含分離區域的情況），因此這類立體也屬於二十面體。例如大二十面體就屬於這種立體。其他的星形二十面體有在同一個面中包含了分離區域的情況，因此可以將這些部分分離成結構更簡單的多面體，這也導致了：雖然這些立體稱為二十面體，但不是嚴格的二十面體。

著名的星形二十面體
凸正	均勻對偶			正複合			星形正	其他
（凸）正二十面體	小三角六边形二十面体	內側三角六邊形二十面體	大三角六邊形二十面體	五複合正八面體	五複合正四面體	十複合正四面體	大二十面體	凹五角錐十二面體	完全星形二十面體
正二十面體在星形化的過程中產生了些許二十面體對稱性的複合多面體

其他常見的二十面體

五角十二面體對稱性的二十面體

五角十二面體對稱性的二十面體

主条目：扭棱四面體

正二十面體可以被形變或標記為對稱性較低的五角十二面體對稱性多面體，形變或標記後的幾何體又稱扭稜八面體（考克斯特扭稜）、扭稜四面體（康威扭稜）或偽二十面體。其也可以視為套用交錯變換的截角八面體。如果所有三角形都是正三角形，那麼也可以透過對8個三角形的三角形組以及12個三角形的三角形組進行著色，分別將這兩組三角形著上不同顏色，以將顏色不同的三角形視為相異的三角形來表達其對稱性。否則，整個立體將與正二十面體無異。

耶森二十面體

主条目：耶森二十面體

與之類似的二十面體還有耶森二十面體。耶森二十面體同樣擁有與正二十面體相同的面數、邊數、頂點數，但其面的形狀、二面角和連接方式略有不同。

• 
  耶森二十面體
• 
  正二十面體（左）與耶森二十面體（右）的差異

耶森二十面體的骨架結構同時也是機器人中常見的张拉整体結構。這種結構早在1980年代已普遍地運用在一種名為Skwish的兒童玩具中。基於這種設計的超級球機器人（super ball bot）也由NASA先進概念研究所提出，預計用於封裝太空設備用於探索其他行星時的著陸方式。

此外，透過將正二十面體的某些三角形以兩兩一組換成2個等腰三角形也能產生類似的幾何形狀，這些形狀有時會被誤認為與正確的耶森二十面體同樣具備张拉整体的特性。事實上，這樣的立體並不具備张拉整体的特性，也不會形成直角的二面角，僅是外觀與耶森二十面體類似而已。

十八角柱

正十八角柱

十八角柱是一種底面為十八邊形的柱體，是二十面體的一種，其由20個面、36個頂點和54個邊組成。正十八角柱代表每個面都是正多邊形的十八角柱，其每個頂點都是2個正方形和1個十八邊形的公共頂點，頂點圖以$4{.}4{.}18$表示，在施萊夫利符號中可以利用{18}×{} 或 t{2, 18}來表示；在考克斯特—迪肯符号中可以利用來表示；在威佐夫符號中可以利用2 18 | 2來表示；在康威多面體表示法中可以利用P18來表示。若正十八角柱底面邊長為$s$、高為$h$，則其體積$V$和表面積$S$為：

$V={\frac {9hs^{2}\cot {\frac {\pi }{18}}}{2}}\approx 25.5208hs^{2}$

$S=9s\left(2h+s\cot {\frac {\pi }{18}}\right)\approx 9s\left(2h+5.67128s\right)$

十九角錐

十九角錐

十九角錐是一種底面為十九邊形的錐體，是二十面體的一種，其具有20個面、38條邊和20個頂點，其對偶多面體是自己本身，因此其也算是自身對偶的多面體之一。正十九角錐是一種底面為正十九邊形的十九角錐。若十九角錐的底面之邊長為$s$、高為$h$則這個正十九角錐的體積$V$和表面積$S$為：

$V={\frac {19hs^{2}\cot {\frac {\pi }{19}}}{12}}\approx 9.4884hs^{2}$

$S={\frac {19s\left({\sqrt {4h^{2}+s^{2}\cot ^{2}{\frac {\pi }{19}}}}+s\cot {\frac {\pi }{19}}\right)}{4}}\approx 3.75s\left({\sqrt {4h^{2}+35.9121s^{2}}}+5.99267s\right)$

菱形二十面體

菱形二十面體

主条目：菱形二十面體

菱形二十面體是一個由20個全等的菱形所組成的環帶多面體。其可以透過移除菱形三十面體的10個中間面來構成。雖然菱形二十面體的20個面皆全等，但其不滿足面可遞的特性，換句話說，即菱形二十面體存在一組兩個面，這兩個面透過將一個面經由若干旋轉、平移和鏡射整個立體將該面的位置變換到另外一個面的位置後，其面與附近的結構並不佔有相同的空間區域。若菱形二十面體的邊長為$a$，則其體積$V$和表面積$S$為：

$V=2{\sqrt {5+2{\sqrt {5}}}}a^{3}$

$S=8{\sqrt {5}}a^{2}$

六角罩帳

正六角罩帳

六角罩帳是指以六邊形為底的罩帳，是一種二十面體，由1個六邊形面、1個十二邊形面、6個五邊形面和12個三角形面組成，共有20個面、42條邊和24個頂點，其中六邊形與十二邊形互相平行，三角形與五邊形交錯地圍繞軸分佈在周圍。其對稱群為C_6v群，階數為12階。

以正六邊形為底的六角罩帳稱為正六角罩帳，其僅有頂面和底面為正多邊形，分別為頂面的正六邊形和底面的正十二邊形，側面可能可以存在正三角形或存在正五邊形，但有正三角形面時，五邊形最多僅能是等邊不等角的非正五邊形；有正五邊形面時，三角形會出現等腰三角形，故不屬於詹森多面體。唯一屬於詹森多面體的罩帳僅有正五角罩帳。

九角反角柱

正九角反角柱

九角反角柱是一種底面為九邊形的反角柱，由20個面、36條邊和18個頂點組成。正九角反角柱代表每個面都是正多邊形的九角反角柱，其每個頂點都是3個正三角形和1個正九邊形的公共頂點，頂點圖以$3{.}3{.}3{.}9$表示，在施萊夫利符號中可以用$s\left\{{\begin{matrix}2\\9\end{matrix}}\right\}$來表示。邊長為單位長的正九角反角柱體積$V$為以下多項式的正實根，約為5.43974：

$64x^{6}-1872x^{4}-648x^{2}+81$

邊長為單位長的正九角反角柱表面積$S$為以下多項式的正實根，約為20.1579：

$x^{6}-486x^{4}+32805x^{2}-177147$

雙十角錐

雙十角錐

雙十角錐是一種以十邊形為基底的雙錐體，是二十面體的一種，其可以視為兩個十角錐底面對底面疊合成的立體，由20個面、30條邊和12個頂點組成。

雙十角錐在施萊夫利符號中可以用{ }+{10}來表示，在考克斯特符號中可以用來表示，在康威多面體表示法中可以用dP10來表示，對偶多面體為十角柱。

十方偏方面體

十方偏方面體是一種以十邊形為基底的偏方面體，由20個全等的鳶形組成，同時也是鳶形多面體，是偏方面體系列的第八個成員。所有十方偏方面體都有20個面、40條邊和22個頂點，其中，頂點有兩種，分別為10個鳶形的公共頂點和3個鳶形的公共頂點。

十方偏方面體是一個等面圖形，即面可遞多面體，其所有面都相等。更具體來說，其不僅所有面都全等，且面與面必須能在其對稱性上傳遞，也就是說，面必須位於同一個對稱性軌道內。這種凸多面體是能做成公正的骰子的形狀，然而二十面骰通常以正二十面體居多。

十方偏方面體在施萊夫利符號中可以用{ }⨁{10}來表示，在考克斯特符號中可以用或來表示，在康威多面體表示法中可以用dA10來表示，對偶多面體為十角反角柱。

星形均勻二十面體

除了星形二十面體之外，還有許多星形多面體屬於二十面體，例如為小立方立方八面體、大立方截半立方體和立方截角立方八面體等。

• 
  小立方立方八面體
• 
  大立方截半立方體
• 
  立方截角立方八面體

小立方立方八面體

小立方立方八面體的立體模型

主条目：小立方立方八面體

小立方立方八面體雖然稱為「八面體」，但其實際為八面體變換後的結果。這個結果恰好具20個面。這種20面體，其二十個面分別為8個正三角形、6個正方形和6個正八邊形，並具有48條邊和24個頂點。小立方立方八面體是一種自相交擬擬正多面體（Self-Intersecting Quasi-Quasi-Regular Polyhedra），由阿爾伯特·巴杜羅（Albert Badoureau）於1881年發現並描述。

大立方截半立方體

大立方截半立方體的立體模型

主条目：大立方截半立方體

大立方截半立方體雖然稱為「立方體」（即一種六面體），但其實際為立方體變換後的結果。更具體的說，變換的原像是截半立方體，並且變換的結果恰好具20個面。這種20面體的20個面包括了8個正三角形、6個正方形和6個八角星，並且由48條邊和24個頂點組成。大立方截半立方體與小立方立方八面體同為20面的自相交擬擬正多面體（Self-Intersecting Quasi-Quasi-Regular Polyhedra），由阿爾伯特·巴杜羅（Albert Badoureau）於1881年發現並描述。

立方截角立方八面體

立方截角立方八面體的立體模型

主条目：立方截角立方八面體

立方截角立方八面體是一種均勻星形二十面體。雖然其被稱為「八面體」，但其實際為八面體變換後的結果。這個結果恰好具20個面。這種20面體，其二十個面分別為8個正六邊形、6個正八邊形和6個正八角星，並具有72條邊和48個頂點組成。立方截角立方八面體與上列兩種均勻星形二十面體（大立方截半立方體、小立方立方八面體）不同。立方截角立方八面體並非自相交擬擬正多面體（Self-Intersecting Quasi-Quasi-Regular Polyhedra），而是一種自相交截角擬正多面體（Self-Intersecting Truncated Quasi-Regular Polyhedra）。其由阿爾伯特·巴杜羅（Albert Badoureau）和約翰·皮奇（Johann Pitsch）於1881年發現並描述。

詹森二十面體

許多詹森多面體是具有20個面的二十面體。例如正三角帳塔反角柱、同相雙三角帳塔柱、異相雙三角帳塔柱、對二側錐十二面體、間二側錐十二面體和三角廣底球狀罩帳。

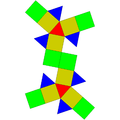
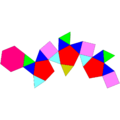
詹森多面體編號	J22	J35	J36	J59	J60	J92
圖像	正三角帳塔反角柱	同相雙三角帳塔柱	異相雙三角帳塔柱	對二側錐十二面體	間二側錐十二面體	三角廣底球狀罩帳
展開圖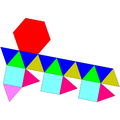
面的組成	16個三角形 3個正方形   1個六邊形	8個三角形 12個正方形	8個三角形 12個正方形	10個三角形   10個五邊形	10個三角形   10個五邊形	13個三角形 3個正方形 3個五邊形 1個六邊形

二十面體列表

名稱	種類	圖像	符號	頂點	邊	面	χ	面的種類	對稱性	展開圖
凸正二十面體	正多面體		{3,5}	12	30	20	2	20個正三角形	Ih, H3, [5,3], (*532)
大二十面體	正多面體		{3,5/2}	12	30	20	2	20個正三角形	Ih, H3, [5,3], (*532)
十八角柱	稜柱體		t{2,18} {18}x{}	54	36	20	2	2個十八邊形 18個矩形	D18h, [18,2], (*18 2 2)
十九角錐	稜錐體		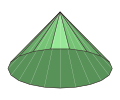( )∨{19}	20	38	20	2	1個十九邊形 19個三角形	C19v, [19], (*19 19)
九角反棱柱	反棱柱		s{2,18} sr{2,9}	18	36	20	2	2個九邊形 18個三角形	D6d, [2+,12], (2*6), 24階
九角帳塔	帳塔		{9}||t{9}	27	45	20	2	9個三角形 9個正方形 1個九邊形 1個十八邊形	C9v, [1,9], (*99), 18階
雙十角錐	雙錐體		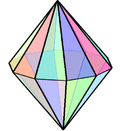{ }+{10}	12	30	20	2	20個三角形	D10h, [10,2], (*10 2 2), 40階
十方偏方面體	偏方面體		{ }⨁{10}	22	40	20	2	20個鷂形	D10d, [2+,10], (2*10)
六角罩帳	罩帳			24	42	20	2	1個六邊形頂面 1個十二邊形底面 6個五邊形側面 12個三角形側面	C6v, [4], (*66), 12階
雙五角錐反角柱	雙錐反柱體			12	30	20	2	20個三角形	D5d, [2+,10], (2*5), order 20

扭歪二十面體

六角四片三角孔扭歪正二十面體是一個扭歪二十面體，其面向鏡頭的正六邊形面已去除。其位於四維空間，圖為四維到三維的施萊格爾投影

扭歪二十面體是指面與頂點並不存在同一個三維空間（共面在四維空間的推廣）而無法確定體積的二十面體，是一種扭歪多面體，所有的扭歪二十面體只能存於四維或以上的空間。例如有一種六維空間的扭歪二十面體。

用途

不同種類的二十面體有不同用途。比方說凸均勻二十面體（如正二十面體和十方偏方面體）可以被製作為骰子；而正二十面體及其五角十二面體對稱性的變體（扭稜四面體）會出現在一些晶體結構、化學物質或生物體結構中。而另一種基於正二十面體改變頂點相連方式構成的耶森二十面體，其骨架結構是機器人中常見的张拉整体結構。其運用包括了兒童玩具的設計、用於封裝太空設備用於探索其他行星時的著陸的機器人等。

參見

• 二十邊形