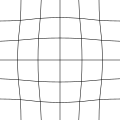
畸變

此條目介紹的是影像上在投影後的變化。關於其他信號的變化，請見「失真」。

幾何光學中的畸變（英語：Distortion）是成像偏離直線投影（直線在投影後仍維持直線的投影），是像差的一種，但和球面像差、彗形像差、色差、佩茲瓦爾像場彎曲及像散不同，後面幾種像差會影響影像的精細度，但不會改變圖案（直線在投影後仍是直線，但會因為像差而變模糊），而畸變會改變圖案本身形狀。畸變與物像點離光軸的垂直高度的立方成正比，因此，物像四角的畸變比物像的四邊的畸變程度大。

分類

桶狀

枕狀

鬍狀

畸變的例子

畸變可能是不規則的，且有許多不同的模式。但很常見的畸變是輻射對稱的，是因為鏡頭的對稱性所產生。這類畸變可以分為桶狀畸變或枕狀畸變。

桶狀畸變

桶狀畸變（barrel distortion）下，影像的放大率隨著和光軸的距離減少。看到的效果是類似影像放在球面（或木桶）上的效果。魚眼鏡頭可以取半個球面的影像，就是利用這種畸變將無窮寬的視野縮到有限的區域內。變焦鏡頭的桶狀畸變出現在一半焦距的位置，在廣角範圍的端點最嚴重。 凹球面透鏡較常出現桶狀畸變。

枕狀畸變

枕狀畸變（pincushion distortion），影像的放大率隨著和光軸的距離增加。視覺的效果是不通過圖形中心的直線會往內彎曲，類似枕形。 凸球面透鏡較常出現枕狀畸變。

鬍狀畸變

鬍狀畸變（mustache distortion）是上述兩種的混合，較少見，但不算非常罕見，在靠近影像中心處是枕狀畸變，往外擴展時慢慢變成枕狀畸變，在圖的上半部的橫線會類似翹八字鬍。

詞語由來

上述畸變的名稱來自有類似外形的日常事物。

• 
  在桶狀畸變中，直線會往外膨脹，類似木桶。
• 
  在枕狀畸變中，方形的四角會往外伸長，類似座墊。
• 
  在鬍狀畸變中，水平線會先在中心部位突出，再往另一個方向彎曲，類似翹八字鬍

出現畸變的情形

globe effect（右邊）和沒有globe effect（左邊）比較的動畫

攝影中的畸變特別和變焦鏡頭有關，特別是大畫幅鏡頭，不過也會在定焦鏡頭上出現，和其焦距有關。例如佳能 EF 50mm 鏡頭 f/1.4 在極短焦距下會有桶狀畸變。廣角鏡頭可能會出現桶狀畸變，且常出現在容易出現在變焦鏡頭的廣角端點，枕狀畸變會出現在較舊或是低階的遠攝鏡頭上。鬍狀畸變特別會在變焦鏡頭的視野末端出現，特別是後焦距鏡頭，最近也在大範圍變焦鏡頭（像是尼康 18–200 mm）上出現。

在光學儀器中（例如雙筒望遠鏡）會有一些枕狀畸變，目的是為了抵消globe effect。

徑向畸變可以由其對同心圓（例如箭靶）的影響來理解

在理解這類畸變時，需記得這些是徑向畸變，探討的光學系統有旋轉對稱（省略非徑向的缺陷），因此正確的測試影像會是一組均勻分隔的同心圓（類似箭靶）。可以看出這些畸變會讓同心圓變成不是均勻分隔。像枕狀畸變就是外圍的圓圈彼此之間的距離會較遠。而桶狀畸變就是外圍的圓圈彼此之間的距離會較近。

軟體修正

有未修正桶狀畸變的圖（26mm）

桶狀畸變已被修正的圖（圖中的電腦是ENIAC電腦）

徑向畸變主要是以低階徑向成份為主，可以用Brown畸變模型來修正，因為Conrady早期的研究，也稱為Brown–Conrady模型。 Brown–Conrady模型可以修正徑向畸變以及因為各鏡頭沒有對正而產生的切線畸變。切線畸變也稱為「離心畸變」。可參考Zhang有關徑向畸變的進一步討論。Brown-Conrady畸變模型為

$${\begin{alignedat}{3}x_{\mathrm {u} }=x_{\mathrm {d} }&+(x_{\mathrm {d} }-x_{\mathrm {c} })(K_{1}r^{2}+K_{2}r^{4}+\cdots )+(P_{1}(r^{2}+2(x_{\mathrm {d} }-x_{\mathrm {c} })^{2})\\&+2P_{2}(x_{\mathrm {d} }-x_{\mathrm {c} })(y_{\mathrm {d} }-y_{\mathrm {c} }))(1+P_{3}r^{2}+P_{4}r^{4}\cdots )\\y_{\mathrm {u} }=y_{\mathrm {d} }&+(y_{\mathrm {d} }-y_{\mathrm {c} })(K_{1}r^{2}+K_{2}r^{4}+\cdots )+(2P_{1}(x_{\mathrm {d} }-x_{\mathrm {c} })(y_{\mathrm {d} }-y_{\mathrm {c} })\\&+P_{2}(r^{2}+2(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}))(1+P_{3}r^{2}+P_{4}r^{4}\cdots ),\end{alignedat}}$$

其中

• $(x_{\mathrm {d} },\ y_{\mathrm {d} })$是用特定透鏡透視到影像平面的畸變影像點
• $(x_{\mathrm {u} },\ y_{\mathrm {u} })$是用理想針孔相機透視到影像平面的無畸變影像點
• $(x_{\mathrm {c} },\ y_{\mathrm {c} })$是畸變中心
• $K_{n}$是第$n$次徑向畸變係數
• $P_{n}$是第$n$次切線畸變係數
• $r$ = ${\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}$，畸變點以及畸變中心的歐幾里得距離

桶狀畸變的$K_{1}$會是負值，而枕狀畸變對應值則是正值。鬍狀畸變會有非單調的徑向畸變幾何數列，在特定的$r$處會變號。

若要為軸向畸變建模，以下的除法模型可以有比Brown-Conrady偶數階模型更準確的結果。

$${\begin{aligned}x_{\mathrm {u} }&=x_{\mathrm {c} }+{\frac {x_{\mathrm {d} }-x_{\mathrm {c} }}{1+K_{1}r^{2}+K_{2}r^{4}+\cdots }}\\y_{\mathrm {u} }&=y_{\mathrm {c} }+{\frac {y_{\mathrm {d} }-y_{\mathrm {c} }}{1+K_{1}r^{2}+K_{2}r^{4}+\cdots }},\end{aligned}}$$

參數和以前定義的相同。針對軸向畸變，此模型比Brown–Conrady模型要好用，需要的項次較少，即可更精確的描述嚴重的畸變。若使用此模型，大部份的相機只需要一項即可描述。

軟體可以用圖像扭轉的作法，對圖像加反向的畸變來復原影像。這需要確認已畸變的像素對應未畸變的哪一個像素，因為模型非線性，此對應不是顯然的。

畸變或去畸變都需要兩組係數，或是找到非線性模型的反函數，一般來言，反函數是沒有解析解的。標準的作法包括近似、局部線性化以及迭代法都可以使用。各精準度以及計算需要的資源各有不同。

若是使用一階的除法模型，其去畸變問題存在解析解，畸變的像素為

$${\begin{aligned}x_{\mathrm {d} }&=x_{\mathrm {c} }+{\frac {x_{\mathrm {u} }-x_{\mathrm {c} }}{2K_{1}r_{u}^{2}}}(1-{\sqrt {1-4K_{1}r_{u}^{2}}})\\y_{\mathrm {d} }&=y_{\mathrm {c} }+{\frac {y_{\mathrm {u} }-y_{\mathrm {c} }}{2K_{1}r_{u}^{2}}}(1-{\sqrt {1-4K_{1}r_{u}^{2}}}),\end{aligned}}$$

其中

• $r_{u}$ = ${\sqrt {(x_{\mathrm {u} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {u} }-y_{\mathrm {c} })^{2}}}$是點相對中心的歐氏距離。

相關條目

• 歪像
• 視角
• 圓柱透視
• 質地梯度
• 水下視覺
• 暈影
• 球面像差