派克轉換

派克轉換（也譯作帕克轉換，英語：Park's Transformation），是目前分析同步電動機及感應馬達執行最常用的一種坐標轉換，由美國工程師羅伯特·H·帕克在1929年提出。派克轉換將定子的a,b,c三相電流投影到隨著轉子旋轉的直軸（d軸），交軸（q軸）與垂直於dq平面的零軸（0軸）上去，從而實現了對定子電感矩陣的對角化，對電動機的執行分析起到了簡化作用。

定義

派克正轉換：

${\mathbf {i} }_{dq0}={\mathbf {P} }{\mathbf {i} }_{abc}={\frac {2}{3}}\left[{\begin{array}{*{20}c}{\cos \theta }&{\cos \left({\theta -120^{\circ }}\right)}&{\cos \left({\theta +120^{\circ }}\right)}\\{-\sin \theta }&{-\sin \left({\theta -120^{\circ }}\right)}&{-\sin \left({\theta +120^{\circ }}\right)}\\{\frac {1}{2}}&{\frac {1}{2}}&{\frac {1}{2}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{i_{a}}\\{i_{b}}\\{i_{c}}\\\end{array}}\right]$

逆轉換：

${\mathbf {i} }_{abc}={\mathbf {P} }^{-1}{\mathbf {i} }_{dq0}=\left[{\begin{array}{*{20}c}{\cos \theta }&{-\sin \theta }&1\\{\cos \left({\theta -120^{\circ }}\right)}&{-\sin \left({\theta -120^{\circ }}\right)}&1\\{\cos \left({\theta +120^{\circ }}\right)}&{-\sin \left({\theta +120^{\circ }}\right)}&1\\\end{array}}\right]\left[{\begin{array}{*{20}c}{i_{d}}\\{i_{q}}\\{i_{0}}\\\end{array}}\right]$

派克轉換也作用在定子電壓與定子繞組磁鏈上： ${\mathbf {u} }_{dq0}={\mathbf {P} }{\mathbf {u} }_{abc}$，${\mathbf {\Psi } }_{dq0}={\mathbf {P} }{\mathbf {\Psi } }_{abc}$

幾何解釋

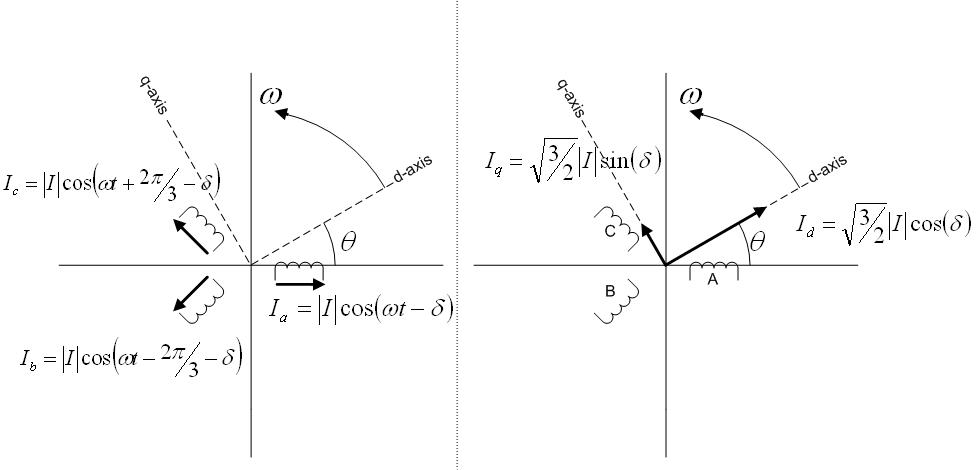
上圖描繪了派克轉換的幾何意義，定子三相電流互成120度角，$\delta$為定子電流落後於它們對應的相電壓的角度。直軸與交軸電流分別等於定子三相電流在d軸與q軸上的投影。（圖中的比例係數${\sqrt {\frac {3}{2}}}$是由於圖中所採用的是正交形式的派克轉換）d-q坐標系在空間中以角速度$\omega$逆時針旋轉，故 $\theta =\omega t$ 以d軸領先a相軸線的方向為正。當定子電流為三相對稱的正弦交流電時，$i_{d}$,$i_{q}$為直流電流，$i_{0}=0$。

用派克轉換化簡同步發電機基本方程式

轉換後的磁鏈方程式

磁鏈方程式：

$\left[{\begin{array}{*{20}c}{{\mathbf {\Psi } }_{abc}}\\{{\mathbf {\Psi } }_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf {L} }_{SS}}&{{\mathbf {L} }_{SR}}\\{{\mathbf {L} }_{RS}}&{{\mathbf {L} }_{RR}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf {i} }_{abc}}\\{{\mathbf {i} }_{fDQ}}\\\end{array}}\right]$

上式中的電感係數矩陣 ${{\mathbf {L} }_{SS}},{{\mathbf {L} }_{SR}},{{\mathbf {L} }_{RS}},{{\mathbf {L} }_{RR}}$ 事實上都含有隨時間變化的角度參數，使得方程式求解困難。

現對等式兩邊同時左乘 $\left[{\begin{array}{*{20}c}{\mathbf {P} }&{}\\{}&{\mathbf {U} }\\\end{array}}\right]$，其中${\mathbf {U} }$為三階單位矩陣。方程式化為：

$\left[{\begin{array}{*{20}c}{{\mathbf {\Psi } }_{dq0}}\\{{\mathbf {\Psi } }_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{\mathbf {P} }&{}\\{}&{\mathbf {U} }\\\end{array}}\right]\left[{\begin{array}{*{20}c}{{\mathbf {L} }_{SS}}&{{\mathbf {L} }_{SR}}\\{{\mathbf {L} }_{RS}}&{{\mathbf {L} }_{RR}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{{\mathbf {P} }^{-1}}&{}\\{}&{\mathbf {U} }\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf {i} }_{abc}}\\{{\mathbf {i} }_{fDQ}}\\\end{array}}\right]$

$\left[{\begin{array}{*{20}c}{{\mathbf {\Psi } }_{dq0}}\\{{\mathbf {\Psi } }_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf {PL} }_{SS}{\mathbf {P} }^{-1}}&{{\mathbf {PL} }_{SR}}\\{{\mathbf {L} }_{RS}{\mathbf {P} }^{-1}}&{{\mathbf {L} }_{RR}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf {i} }_{dq0}}\\{{\mathbf {i} }_{fDQ}}\\\end{array}}\right]$

其中 ${\mathbf {PL} }_{SS}{\mathbf {P} }^{-1}=\left[{\begin{array}{*{20}c}{L_{d}}&{}&{}\\{}&{L_{q}}&{}\\{}&{}&{L_{0}}\\\end{array}}\right]\triangleq {\mathbf {L} }_{dq0}$。

① 轉換後的電感係數都變為常數，可以假想dd繞組，qq繞組是固定在轉子上的，相對轉子靜止。

② 派克轉換陣對定子自感矩陣 ${\mathbf {L} }_{SS}$ 起到了對角化的作用，並消去了其中的角度變數。${L_{d}},{L_{q}},{L_{0}}$ 為其特徵根。

③ 轉換後定子和轉子間的互感係數不對稱，這是由於派克轉換的矩陣不是正交矩陣。

④ ${L_{d}}$ 為直軸同步電感係數，其值相當於當勵磁繞組開路，定子合成磁勢產生單純直軸磁場時，任意一相定子繞組的自感係數。

轉換後的電壓方程式

電壓方程式：

$\left[{\begin{array}{*{20}c}{{\mathbf {U} }_{abc}}\\{{\mathbf {U} }_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf {r} }_{S}}&{}\\{}&{{\mathbf {r} }_{R}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf {i} }_{abc}}\\{{\mathbf {i} }_{fDQ}}\\\end{array}}\right]+\left[{\begin{array}{*{20}c}{{\mathbf {\dot {\Psi }} }_{abc}}\\{{\mathbf {\dot {\Psi }} }_{fDQ}}\\\end{array}}\right]$

現對等式兩邊同時左乘 $\left[{\begin{array}{*{20}c}{\mathbf {P} }&{}\\{}&{\mathbf {U} }\\\end{array}}\right]$，其中${\mathbf {U} }$為三階單位矩陣。方程式化為：

$\left[{\begin{array}{*{20}c}{{\mathbf {U} }_{dq0}}\\{{\mathbf {U} }_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf {r} }_{S}}&{}\\{}&{{\mathbf {r} }_{R}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf {i} }_{dq0}}\\{{\mathbf {i} }_{fDQ}}\\\end{array}}\right]+\left[{\begin{array}{*{20}c}{{\mathbf {P{\dot {\Psi }}} }_{abc}}\\{{\mathbf {\dot {\Psi }} }_{fDQ}}\\\end{array}}\right]$

由 ${\mathbf {\Psi } }_{dq0}={\mathbf {P\Psi } }_{abc}$ ，

對兩邊求導，得 ${\mathbf {\dot {\Psi }} }_{dq0}={\mathbf {{\dot {P}}\Psi } }_{abc}+{\mathbf {P{\dot {\Psi }}} }_{abc}$ ，

所以 ${\mathbf {P{\dot {\Psi }}} }_{abc}={\mathbf {\dot {\Psi }} }_{dq0}-{\mathbf {{\dot {P}}\Psi } }_{abc}={\mathbf {\dot {\Psi }} }_{dq0}-{\mathbf {{\dot {P}}P} }^{-1}{\mathbf {\Psi } }_{dq0}$

其中 ${\mathbf {{\dot {P}}P} }^{-1}=\left[{\begin{array}{*{20}c}{}&\omega &{}\\{-\omega }&{}&{}\\{}&{}&{}\\\end{array}}\right]$ ，令 ${\mathbf {S} }={\mathbf {{\dot {P}}P} }^{-1}{\mathbf {\Psi } }_{dq0}=\left[{\begin{array}{*{20}c}{}&\omega &{}\\{-\omega }&{}&{}\\{}&{}&{}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{\Phi _{d}}\\{\Phi _{q}}\\{\Phi _{0}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{\omega \Psi _{q}}\\{-\omega \Psi _{d}}\\{}\\\end{array}}\right]$

於是有 $\left[{\begin{array}{*{20}c}{{\mathbf {U} }_{dq0}}\\{{\mathbf {U} }_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf {r} }_{S}}&{}\\{}&{{\mathbf {r} }_{R}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf {i} }_{dq0}}\\{{\mathbf {i} }_{fDQ}}\\\end{array}}\right]+\left[{\begin{array}{*{20}c}{{\mathbf {\dot {\Psi }} }_{dq0}}\\{{\mathbf {\dot {\Psi }} }_{fDQ}}\\\end{array}}\right]-\left[{\begin{array}{*{20}c}{\mathbf {S} }\\{}\\\end{array}}\right]$

上式右邊第一項為繞組電阻的壓降，第二項為變壓器電勢，第三項為發電機電勢或旋轉電勢。

相關條目

• 向量控制
• 克拉克變換

參考書目

• 電機電子類科《電力系統暫態分析》，ISBN 978-7-5083-4825-4，作者：李光琦，中國電力出版社。