 這個函數不是凸的,但是是擬凸的
這個函數不是凸的,但是是擬凸的
 這個函數不是擬凸的
這個函數不是擬凸的
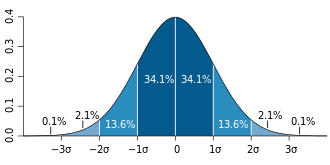 正態分布的概率密度函數是擬凹的,但不是凹的
正態分布的概率密度函數是擬凹的,但不是凹的
擬凸函數(Quasiconvex function)是一類定義在實向量空間的區間或凸子集上的實值函數,且滿足對任意實數 ,
, 的原像都是凸集。反之如果原像都是凹集,則稱為擬凹函數。
的原像都是凸集。反之如果原像都是凹集,則稱為擬凹函數。
凸函數一定是擬凸函數,但反之則不然,因此擬凸函數是一個更廣泛的概念。凹函數的情況也類似。
設函數 定義在實向量空間的凸子集
定義在實向量空間的凸子集 上。我們稱
上。我們稱 是擬凸的,如果對任意的
是擬凸的,如果對任意的 和
和![{\displaystyle \lambda \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/010c0ee88963a09590dd07393d288edd83786b91) 都有
都有
 。
。
另一種等價的定義則是任何的 都是凸集。
都是凸集。
如果有 ,則稱
,則稱 是嚴格擬凸的。
是嚴格擬凸的。
類似地,可以定義擬凹函數和嚴格擬凹函數。我們稱 是擬凹的,如果對任意的
是擬凹的,如果對任意的 和
和![{\displaystyle \lambda \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/010c0ee88963a09590dd07393d288edd83786b91) 都有
都有
 。
。
如果有 ,則稱
,則稱 是嚴格擬凹的。
是嚴格擬凹的。
如果一個函數既是擬凸的又是擬凹的,則稱其為擬線性的。










![{\displaystyle \lambda \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/010c0ee88963a09590dd07393d288edd83786b91)




