投影切片定理

在數學上，二維情況下的投影切片定理（英語：projection-slice theorem）（或稱中心切片定理，英語：central slice theorem、傅立葉切片定理，英語：Fourier slice theorem）表明以下兩個運算的結果相等：

• 將二維函數$f\left(\mathbf {r} \right)$先投影到一維的線上（即進行拉東變換），並對投影結果進行傅立葉變換。
• 對相同的函數先進行二維傅立葉變換，然後通過平行於投影線的原點對其進行切片。

以算子形式表示，令：

• $F_{1}$和$F_{2}$分別為一維和二維傅立葉變換算子
• $P_{1}$為投影算子（即將二維函數投影為一維的線）
• $S_{1}$為切片算子（從函數中通過原點提取一維切片）

則有：

$F_{1}P_{1}=S_{1}F_{2}$

以上結論可以推廣到高維情況。

該定理可以應用於醫學CT掃描中，此時，「投影」是對體內器官的X光成像。對成像結果的傅立葉變換可以看作是體內器官三維密度的傅立葉變換的切片，而這些切片通過插值可以構造密度的完整傅立葉變換。對得到的完整結果應用傅立葉逆變換可以得到目標體的密度。這一技術由羅納德·布雷斯韋爾於1956年為射電天文學問題開發。

N維的投影切片定理

在N維情況下，投影切片定理表明N維函數$f\left(\mathbf {r} \right)$投影於m維線性子流形的傅立葉變換等同於該函數N維傅立葉變換的m維切片，切片由m維的線性子流形組成，該流形穿過傅立葉空間中的原點，並平行於投影子流形。以算子形式表示該定理，則有：

$F_{m}P_{m}=S_{m}F_{N}.\,$

傅立葉切片定理的推廣

除了推廣到N維空間外，投影切片定理還可以通過改變基函數得到進一步推廣。為了方便表示，我們將基的變化表示為矩陣$B$，該矩陣為大小為$N\times N$的可逆矩陣。廣義傅立葉切片定理則可以表示為：

$F_{m}P_{m}B=S_{m}{\frac {B^{-T}}{|B^{-T}|}}F_{N}$

其中$B^{-T}=(B^{-1})^{T}$是對基變換矩陣$B$求逆的轉置。

二維情況下的證明

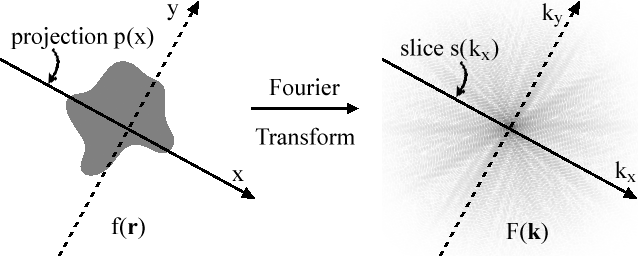二維投影切片定理的圖示。$f\left(\mathbf {r} \right)$和$F\left(\mathbf {k} \right)$ 是二維傅立葉變換對。$f\left(\mathbf {r} \right)$在 x 軸上的投影是$f\left(\mathbf {r} \right)$沿平行於 y 軸的方向的線積分，記為$p\left(x\right)$。通過$F\left(\mathbf {k} \right)$的切片位於$k_{x}$ 軸上，該軸平行於$x$ 軸並，記為 $s\left(k_{x}\right)$。投影切片定理指出$p\left(x\right)$ 和$s\left(k_{x}\right)$ 是一維傅立葉變換對。

二維的情況下的投影切片定理容易證明。此處取投影線作為 x 軸，由於可以通過平移和旋轉變換投影線到x軸上，所該選取方式具有普遍性。

設$f\left(x,y\right)$為二維函數，其在x軸方向方向上的投影$p\left(x\right)$為：

$p(x)=\int _{-\infty }^{\infty }f(x,y)\,dy.$

$f\left(x,y\right)$的二維傅立葉變換為：

$F(k_{x},k_{y})=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\,e^{-2\pi i(xk_{x}+yk_{y})}\,dxdy.$

在傅立葉域的切片$s(k_{x})$為：

$s(k_{x})=F(k_{x},0)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\,e^{-2\pi ixk_{x}}\,dxdy$

$=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }f(x,y)\,dy\right]\,e^{-2\pi ixk_{x}}dx$

$=\int _{-\infty }^{\infty }p(x)\,e^{-2\pi ixk_{x}}dx$

其正是$p\left(x\right)$的傅立葉變換。更高維的證明可以從以上例子中推廣得到。

FHA（Fourier-Hankel-Abel）循環

如果二維函數 $f\left(\mathbf {r} \right)$是圓對稱的，它可以表示為$f\left(r\right)$，其中$r=\left|\mathbf {r} \right|$。此時，投影到任何投影線上都是$f\left(r\right)$的阿貝爾變換。$f\left(\mathbf {r} \right)$ 的二維傅立葉變換等價於$f\left(r\right)$零階漢克爾變換給出的圓對稱函數，因此它也將表示通過原點的任何切片。投影切片定理指出，投影的傅立葉變換等同於傅立葉變換的切片，以算子形式表示為：

$F_{1}A_{1}=H,$

其中$A_{1}$表示阿貝爾變換算子，將二維圓對稱函數投影到一維的線上，$F_{1}$表示一維傅立葉變換算子，$H$表示零階漢克爾變換算子。

扇形束和錐形束CT的推廣

投影切片定理適用於具有平行束投影的CT圖像重建，但其並不適用於扇形束或錐形束的CT。該定理於1995年被Shuang-ren Zhao擴展到了扇形束和錐形束CT圖像重建。

參見

• 拉東變換#與傅立葉變換的關係