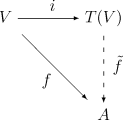在數學中,一個向量空間 的張量代數(tensor algebra),記作
的張量代數(tensor algebra),記作 ,是
,是 上的(任意階)張量的代數,其乘法為張量積。張量代數左伴隨於從代數到向量空間的遺忘函子,在這種意義下它是
上的(任意階)張量的代數,其乘法為張量積。張量代數左伴隨於從代數到向量空間的遺忘函子,在這種意義下它是 上的自由代數;在相應的泛性質的意義下,它是包含
上的自由代數;在相應的泛性質的意義下,它是包含 的「最一般的代數」(見下)。
的「最一般的代數」(見下)。
張量代數也具有余代數結構。
注:本文中所有代數都假設是有單位的且結合。
設 是域
是域 上一個向量空間。對任何非負整數
上一個向量空間。對任何非負整數 ,我們定以
,我們定以 的
的 次張量積為
次張量積為 與自己的
與自己的 次張量積:
次張量積:
 。
。
這便是講, 由
由 上所有秩
上所有秩 張量組成。習慣上
張量組成。習慣上 是基域
是基域 (作為自己的一維向量空間)。
(作為自己的一維向量空間)。
令 為所有
為所有 (
( )的直和:
)的直和:
 。
。
 中的乘法由典範同構確定:
中的乘法由典範同構確定:

由張量積給出,然後線性擴張到所有 。此乘法表明張量代數
。此乘法表明張量代數 自然是一個分次代數,
自然是一個分次代數, 作為
作為 次子空間。
次子空間。
此構造可徑直推廣到任意交換環上的模 上。如果
上。如果 是一個非交換環,我們仍然可以對任意
是一個非交換環,我們仍然可以對任意 -
- 雙模執行這樣的構造。(對通常的
雙模執行這樣的構造。(對通常的 -模不行,因為沒有迭代張量積。)
-模不行,因為沒有迭代張量積。)
張量代數 也成為向量空間
也成為向量空間 上的自由代數,並具有函子性。像其它自由構造一樣,函子
上的自由代數,並具有函子性。像其它自由構造一樣,函子 左伴隨於某個遺忘函子,該函子將每個
左伴隨於某個遺忘函子,該函子將每個 -代數送到它的底向量空間。
-代數送到它的底向量空間。
準確地說,張量代數滿足如下的泛性質,正式地表明它是包含 的最一般的代數:
的最一般的代數:
- 任何從
 到
到 上的一個代數
上的一個代數 的線性變換
的線性變換 可以惟一地擴張為從
可以惟一地擴張為從 到
到 的一個代數同態,如下交換圖表所示:
的一個代數同態,如下交換圖表所示:
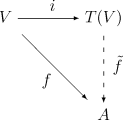 張量代數的泛性質
張量代數的泛性質
這裡 是
是 到
到 的典範包含(伴隨的單位)。事實上可以定義張量代數
的典範包含(伴隨的單位)。事實上可以定義張量代數 為滿足這個性質惟一的代數(確切地說,在惟一的一個同構意義下),但仍然要證明滿足這個性質的對象存在。
為滿足這個性質惟一的代數(確切地說,在惟一的一個同構意義下),但仍然要證明滿足這個性質的對象存在。
如上泛性質說明張量代數的構造有自然的函子性。就是講, 是從
是從 -Vect,
-Vect, 上向量空間範疇,到
上向量空間範疇,到 -Alg,
-Alg, -代數範疇,的一個函子。
-代數範疇,的一個函子。 的函子性意味著任何從V到W的線性映射惟一地擴張為從
的函子性意味著任何從V到W的線性映射惟一地擴張為從 到
到 的代數同態。
的代數同態。
如果 為有限維
為有限維 ,張量代數的另一個看法是「
,張量代數的另一個看法是「  上
上 個非交換變量的多項式代數」。如果我們取
個非交換變量的多項式代數」。如果我們取 的基向量,它們成為
的基向量,它們成為 中的非交換變量(或不定元),彼此間沒有任何約束(除了結合律,分配律以及K-線性)。
中的非交換變量(或不定元),彼此間沒有任何約束(除了結合律,分配律以及K-線性)。
注意 上的多項式代數不是
上的多項式代數不是 ,而是
,而是 :
: 上一個(齊次)線性函數是
上一個(齊次)線性函數是 中的一個元素。
中的一個元素。
因為張量代數的一般性,許多其它有趣的代數可以由張量代數開始構造,然後在生成元上施以一定的關係,即構造 一定的商代數。這樣的例子譬如外代數、對稱代數、克利福德代數以及泛包絡代數。
一定的商代數。這樣的例子譬如外代數、對稱代數、克利福德代數以及泛包絡代數。
張量代數上的余代數結構如下。余積 定義為
定義為

線性擴張到整個 。余單位由
。余單位由 的0-次分量。注意到
的0-次分量。注意到 保持分次:
保持分次:

而 也與分次相容。
也與分次相容。
張量代數在這個余積下不是雙代數。但下述更複雜的余積確實得到一個余代數:

這裡求和取遍所有(p,m-p)-牌序。最後,對極映射為:

線性擴張到整個 ,這樣張量代數成為一個霍普夫代數。
,這樣張量代數成為一個霍普夫代數。
- 陳維桓. 微分流形初步 第二版. 北京: 高等教育出版社. 2001年8月.
- Mac Lane, Saunders. Categories for the Working Mathematician(2nd ed.). GTM5. Spinger, 1998