反正弦

反正弦
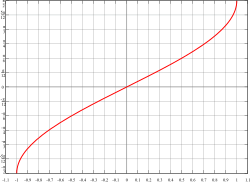性質
奇偶性	奇
定義域	[-1, 1]
到達域	$\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]$ （[-90°,90°]）
周期	N/A
特定值
當x=0	0
當x=+∞	N/A
當x=-∞	N/A
最大值	${\frac {\pi }{2}}$ （90°）
最小值	$-{\frac {\pi }{2}}$ （-90°）
其他性質
漸近線	N/A
根	0
拐點	原點
不動點	0

反正弦（arcsine，$\arcsin$，$\sin ^{-1}$）是一種反三角函數，也是高等數學中的一種基本特殊函數。在三角學中，反正弦被定義為一個角度，也就是正弦值的反函數。在實數域$\mathbb {R}$內，正弦函數的值域為$\left[-1,1\right]$，不是一個雙射函數，故在整個定義域上無法有單值的反函數；但若限定正弦函數的定義域在$\left[-{\frac {\pi }{2}}+k\pi ,{\frac {\pi }{2}}+k\pi \right]$（$[180^{\circ }k-90^{\circ },180^{\circ }k+90^{\circ }]$）內，則正弦函數有反函數。在實數域內，通常將反正弦函數的定義域限制在區間$\left[-1,1\right]$，值域限制在區間$\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]$（$[-90^{\circ },90^{\circ }]$）中；若利用自然對數，則可將反正弦函數的定義域擴充至整個複數集，但這樣一來反正弦函數也將變成多值函數。

命名

反正弦的符號是arcsin，也常常寫作$\sin ^{-1}$。如此寫法可以被接受的理由是，正弦函數的倒數是餘割，有單獨的寫法，因此不易和$\sin ^{-1}$混淆。另外在某些計算機的按鍵或電腦的編程語言中，反正弦會以asin或asn表示。

定義

原始的定義是將正弦函數限制在$\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]$（$[-90^{\circ },90^{\circ }]$）的反函數，得到如下定義域和值域：

$\arcsin :\left[-1,1\right]\rightarrow \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]$

（$\arcsin :\left[-1,1\right]\rightarrow \left[-90^{\circ },90^{\circ }\right]$）

利用自然對數可將定義推廣到整個複數集：

$\arcsin x=-{\mathrm {i} }\ln \left({\mathrm {i} }x+{\sqrt {1-x^{2}}}\right)\,$

拓展到複數的反正弦函數

運算

反正弦函數的導數是：

${\frac {d}{dx}}\arcsin x={\frac {1}{\sqrt {1-x^{2}}}}$

故實數域內，它在整個定義域上單調遞增。

反正弦函數的泰勒級數是：

$\arcsin x=\sum _{k=0}^{\infty }{-{\frac {1}{2}} \choose k}(-1)^{k}{\frac {x^{2k+1}}{2k+1}}=x+{\frac {1}{6}}x^{3}+{\frac {3}{40}}x^{5}+{\frac {5}{112}}x^{7}+\cdots$.

反正弦函數是奇函數，故：

$\arcsin \left(-x\right)=-\arcsin x$

另外，反正弦的和差也可以合併成一個反正弦來表達：

$\arcsin x_{1}\pm \arcsin x_{2}={\begin{cases}X&\pm x_{1}x_{2}\leq 0\lor x_{1}^{2}+x_{2}^{2}\leq 1\\\pi -X&x_{1}>0\land \pm x_{2}>0\land x_{1}^{2}+x_{2}^{2}>1\\-\pi -X&x_{1}<0\land \pm x_{2}<0\land x_{1}^{2}+x_{2}^{2}>1\end{cases}}$

其中$X=\arcsin \left(x_{1}{\sqrt {1-x_{2}^{2}}}\pm x_{2}{\sqrt {1-x_{1}^{2}}}\right)$。

和差公式：

$\arcsin(x\pm y)=\arcsin \left({\sqrt {\frac {1+x^{2}-y^{2}-{\sqrt {1+x^{4}+y^{4}-2x^{2}y^{2}-2x^{2}-2y^{2}}}}{2}}}\right)\pm \arcsin \left({\sqrt {\frac {1-x^{2}+y^{2}-{\sqrt {1+x^{4}+y^{4}-2x^{2}y^{2}-2x^{2}-2y^{2}}}}{2}}}\right)$

倍變數公式：

$\arcsin(2x)=2\arcsin \left({\sqrt {\frac {1-{\sqrt {1-4x^{2}}}}{2}}}\right)$

$\arcsin \left({\frac {x}{2}}\right)=2\arcsin \left({\sqrt {\frac {1-{\sqrt {1-{\frac {x^{2}}{4}}}}}{2}}}\right)$

$\arcsin(kx)=2\arcsin \left({\sqrt {\frac {1-{\sqrt {1-k^{2}x^{2}}}}{2}}}\right)$（對0 ≤ kx ≤ 1）

$\arcsin(sinx)={\begin{cases}-(X+\pi )&x\in [-\pi ,-{\frac {\pi }{2}}]\\X&x\in (-{\frac {\pi }{2}},{\frac {\pi }{2}})\\\pi -X&x\in [{\frac {\pi }{2}},\pi ]\end{cases}}$

參見

• 正弦
• 反餘弦