QMA

在計算複雜性理論中，QMA（英語：Quantum Merlin Arthur，意為量子梅林-亞瑟）是一個複雜性類，它包含了這樣一類決策問題：對於一個答案為「是」的實例，證明者（梅林）可以提供一個多項式大小的量子證明（一個量子態），使驗證者（亞瑟）在多項式時間內能夠以高概率確信其為「是」（這被稱為完備性）；反之，對於答案為「否」的實例，任何證明都將以高概率被驗證者拒絕（這被稱為可靠性）。

QMA 與 BQP 的關係，可類比於經典複雜性類中 NP 與 P 的關係，以及概率複雜性類中 MA 與 BPP 的關係。

定義

一個語言 $L$ 屬於 ${\mathsf {QMA}}(c,s)$，如果存在一個多項式時間量子驗證者 $V$ 和一個多項式 $p(n)$（其中 $n$ 為輸入 $x$ 的長度），滿足：

• 對於所有 $x\in L$，存在一個量子態 $|\psi \rangle$，使得驗證者 $V$ 接受輸入 $(|x\rangle ,|\psi \rangle )$ 的概率大於 $c$。
• 對於所有 $x\notin L$，以及所有最多包含 $p(|x|)$ 個量子比特的量子態 $|\psi \rangle$，驗證者 $V$ 接受輸入 $(|x\rangle ,|\psi \rangle )$ 的概率小於 $s$。

複雜性類 ${\mathsf {QMA}}$ 被定義為等於 ${\mathsf {QMA}}(2/3,1/3)$。然而，這些常數並不十分重要，因為如果將 $c$ 和 $s$ 設置為任何滿足 $c>s$ 的常數，該複雜性類保持不變。此外，對於任何多項式 $q(n)$ 和 $r(n)$，我們有：$${\mathsf {QMA}}\left({\frac {2}{3}},{\frac {1}{3}}\right)={\mathsf {QMA}}\left({\frac {1}{2}}+{\frac {1}{q(n)}},{\frac {1}{2}}-{\frac {1}{q(n)}}\right)={\mathsf {QMA}}(1-2^{-r(n)},2^{-r(n)})$$

QMA中的問題

由於許多有意義的複雜性類，如P、BQP和NP，都包含在QMA中，所以這些類中的所有問題也都在QMA中。然而，存在一些問題屬於QMA，但目前尚不知道它們是否屬於NP或BQP。下面將討論一些這類著名的問題。

一個問題被稱為QMA困難（QMA-hard），類似於NP困難，如果QMA中的每個問題都可以歸約到它。如果一個問題是QMA困難的並且屬於QMA，則稱其為QMA完全（QMA-complete）的。

局域哈密頓量問題

一個k-局域哈密頓量（k-local Hamiltonian） $H$ 是一個作用於 $n$ 個量子比特的厄米矩陣，它可以表示為 $m$ 個哈密頓量項的總和，每個項最多作用於 $k$ 個量子比特。$$H=\sum _{i=1}^{m}H_{i}$$一般的k-局域哈密頓量問題是，給定一個k-局域的哈密頓量 $H$，找出 $H$ 的最小本徵值 $\lambda$。 $\lambda$ 也稱為該哈密頓量的基態能量。

k-局域哈密頓量問題的判定版本是一種承諾問題，定義為：給定一個k-局域哈密頓量和兩個實數 $\alpha ,\beta$ 且 $\alpha >\beta$，判斷是否存在 $H$ 的一個量子本徵態 $|\psi \rangle$，其對應的本徵值 $\lambda$ 滿足 $\lambda \leq \beta$，或者是否對於所有本徵態其本徵值 $\lambda \geq \alpha$。

局域哈密頓量問題是MAX-SAT的量子對應物。對於 $k\geq 2$，k-局域哈密頓量問題是QMA完全的。

限制在二維量子比特網格上作用的2-局域哈密頓量問題也是QMA完全的。 研究表明，即使對於表示一維粒子鏈且每個粒子具有12個狀態的最近鄰相互作用哈密頓量，k-局域哈密頓量問題仍然是QMA困難的。如果系統是平移不變的，其局域哈密頓量問題變為QMA_EXP-完全（因為問題輸入被編碼在系統大小中，驗證者現在具有指數級運行時間，同時保持相同的承諾間隙）。

目前已知，一些簡單的量子比特晶格模型，如ZX哈密頓量，具有QMA困難性（QMA-hardness）：$$H_{ZX}=\sum _{i}h_{i}Z_{i}+\sum _{i}\Delta _{i}X_{i}+\sum _{i<j}J^{ij}Z_{i}Z_{j}+\sum _{i<j}K^{ij}X_{i}X_{j}$$其中 $Z,X$ 代表泡利矩陣 $\sigma _{z},\sigma _{x}$。這類模型適用於普適絕熱量子計算。

k-局域哈密頓量問題類似於經典的約束滿足問題。下表說明了經典約束滿足問題和哈密頓量之間的類似組件。

經典	量子	註釋
約束滿足問題	哈密頓量
變量	量子比特
約束	哈密頓量項
變量賦值	量子態
滿足的約束數量	哈密頓量的能量項
最優解	哈密頓量的基態	滿足儘可能多的約束

其他QMA完全問題

已知的QMA完全問題列表可在 https://arxiv.org/abs/1212.6312 找到。

相關類別

QAM（Quantum Arthur Merlin）是一個與 QMA 密切相關的變體。在 QAM 協議中，驗證者亞瑟首先向證明者梅林發送一個隨機字符串（即「公共硬幣」），梅林再以此為依據提供證明。

QCMA（Quantum Classical Merlin Arthur，有時也寫作MQA，對應Merlin Quantum Arthur）與QMA類似，其核心區別在於證明方（梅林）提供的證明必須是一個經典字符串，而非量子態。目前尚不清楚QMA是否等同於QCMA，儘管QCMA顯然是QMA的一個子集（即${\mathsf {QCMA}}\subseteq {\mathsf {QMA}}$）。

QIP(k) 全稱為「量子交互式多項式時間（k條消息）」（Quantum Interactive Polynomial time (k messages)），可以看作是QMA的推廣。在該模型中，梅林（證明者）和亞瑟（驗證者）可以進行 $k$ 輪交互。因此，QMA本質上就是QIP(1)（即只有一輪交互，梅林發送證明，亞瑟進行驗證）。目前已知 QIP(2)（兩輪交互）包含在複雜性類PSPACE中。

QIP 則代表「量子交互式證明」（Quantum Interactive Proof），它與QIP(k)類似，但允許交互的輪數$k$是輸入規模（例如量子比特數量）的多項式函數。研究表明，只需三輪交互就足以達到QIP的全部計算能力，即 ${\mathsf {QIP}}(3)={\mathsf {QIP}}$。 此外，一個重要的結論是，QIP與經典的交互式證明系統 IP 以及PSPACE等價，即 ${\mathsf {QIP}}={\mathsf {IP}}={\mathsf {PSPACE}}$。

與其他複雜性類的關係

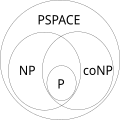
QMA與其他已知的複雜性類的關係如下：$${\mathsf {P}}\subseteq {\mathsf {NP}}\subseteq {\mathsf {MA}}\subseteq {\mathsf {QCMA}}\subseteq {\mathsf {QMA}}\subseteq {\mathsf {PP}}\subseteq {\mathsf {PSPACE}}$$第一個包含關係源於NP的定義。接下來的兩個包含關係是因為驗證者在每種情況下都變得更強大。QCMA包含在QMA中，因為驗證者可以通過在接收到證明後立即進行測量來強制證明者發送經典證明。QMA包含在PP中的事實由阿列克謝·基塔耶夫（Alexei Kitaev）和約翰·沃特羅斯（John Watrous）證明。PP也很容易證明包含在PSPACE中。

目前尚不清楚這些包含關係是否有任何一個是嚴格的，因為甚至連P是否嚴格包含在PSPACE中（即P = PSPACE是否成立）都未知。然而，目前已知的QMA的最佳上界是： ${\mathsf {QMA}}\subseteq {\mathsf {A_{0}PP}}$ 且 ${\mathsf {QMA}}\subseteq {\mathsf {P^{QMA[log]}}}$，其中 ${\mathsf {A_{0}PP}}$ 和 ${\mathsf {P^{QMA[log]}}}$ 都包含在 ${\mathsf {PP}}$ 中。 ${\mathsf {QMA}}$ 不太可能等於 ${\mathsf {P^{QMA[log]}}}$，因為這將意味着 ${\mathsf {QMA}}={\mathsf {co}}$-${\mathsf {QMA}}$。目前尚不清楚 ${\mathsf {P^{QMA[log]}}}\subseteq {\mathsf {A_{0}PP}}$ 或反之是否成立。

外部連結

• Aaronson, Scott. PHYS771 Lecture 13: How Big are Quantum States?. 
• Gharibian, Sevag. Lecture 5: Quantum Merlin Arthur (QMA) and strong error reduction (PDF). 
• Complexity Zoo:Q - Complexity Zoo. complexityzoo.net. [2025-05-22].