FMT='"`UNIQ--nowiki-00000000-QINU`"'; ID=foo; LBL=bar; UST=%Lnowiki%G{{=}} 5%Lnowiki%G'%L/nowiki%G%L/nowiki%G; SUB=<nowiki>{{=}} 5<nowiki>'</nowiki></nowiki>; EXP='"`UNIQ--nowiki-00000001-QINU`"'</nowiki>;✶
{{=}} 5<nowiki>'</nowiki>
FMT='"`UNIQ--nowiki-00000004-QINU`"'; ID=foo; LBL=bar; UST='"`UNIQ--nowiki-00000003-QINU`"'; SUB='"`UNIQ--nowiki-00000003-QINU`"'; EXP='"`UNIQ--nowiki-00000003-QINU`"';✶
=
FMT='"`UNIQ--nowiki-00000007-QINU`"'; ID=foo; LBL=bar; UST='"`UNIQ--nowiki-00000006-QINU`"'; SUB='"`UNIQ--nowiki-00000006-QINU`"'; EXP='"`UNIQ--nowiki-00000006-QINU`"';✶
{{=}}
FMT='"`UNIQ--nowiki-00000009-QINU`"'; ID=foo; LBL=bar; UST={{#tag:nowiki|{{=}}}}; SUB={{#tag:nowiki|{{=}}}}; EXP='"`UNIQ--nowiki-0000000A-QINU`"';✶
=
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
FMT='"`UNIQ--nowiki-00000010-QINU`"'; ID=math_'"`UNIQ--nowiki-0000000E-QINU`"'; LBL='"`UNIQ--nowiki-0000000E-QINU`"'; UST=[[#{{#invoke:decodeEncode|encode|s={{UnstripNoWiki|%i}}|charset=]}}|%l]]; SUB=[[#{{#invoke:decodeEncode|encode|s={{UnstripNoWiki|math_'"`UNIQ--nowiki-0000000E-QINU`"'}}|charset=]}}|'"`UNIQ--nowiki-0000000E-QINU`"']]; EXP=[[#math_x90]]" style=|'"`UNIQ--nowiki-0000000E-QINU`"']];✶
x90]]" style=
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
FMT='"`UNIQ--nowiki-00000016-QINU`"'; ID=math_'"`UNIQ--nowiki-00000014-QINU`"'; LBL='"`UNIQ--nowiki-00000014-QINU`"'; UST=[[#{{#invoke:decodeEncode|encode|charset='{{(}}{{)}}{{=}}|s={{UnstripNoWiki|%i}}}}|%l]]; SUB=[[#{{#invoke:decodeEncode|encode|charset='{{(}}{{)}}{{=}}|s={{UnstripNoWiki|math_'"`UNIQ--nowiki-00000014-QINU`"'}}}}|'"`UNIQ--nowiki-00000014-QINU`"']]; EXP=[[#math_{{=}} 89''|'"`UNIQ--nowiki-00000014-QINU`"']];✶
{{=}} 89''
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
FMT='"`UNIQ--nowiki-0000001B-QINU`"'; ID=math_'"`UNIQ--nowiki-00000019-QINU`"'; LBL='"`UNIQ--nowiki-00000019-QINU`"'; UST=[[#{{UnstripNoWiki|%i}}|{{#invoke:decodeEncode|encode|s={{UnstripNoWiki|%l}}}}]]; SUB=[[#{{UnstripNoWiki|math_'"`UNIQ--nowiki-00000019-QINU`"'}}|{{#invoke:decodeEncode|encode|s={{UnstripNoWiki|'"`UNIQ--nowiki-00000019-QINU`"'}}}}]]; EXP=[[#math_67''|67'']];✶
67''
abc[s][s]defg
FMT='"`UNIQ--nowiki-0000001D-QINU`"'; ID=math_'"`UNIQ--nowiki-0000001E-QINU`"'; LBL='"`UNIQ--nowiki-0000001F-QINU`"'; UST={{#invoke:string|replace|[[{{UnstripNoWiki|#%i}}|%l]]|%%s||99|false}}; SUB={{#invoke:string|replace|[[{{UnstripNoWiki|#math_'"`UNIQ--nowiki-0000001E-QINU`"'}}|'"`UNIQ--nowiki-0000001F-QINU`"']]|%s||99|false}}; EXP=[[#math_=78''|'"`UNIQ--nowiki-0000001F-QINU`"']];✶
{{=}} 8''
FMT='"`UNIQ--nowiki-00000021-QINU`"'; ID=math_'"`UNIQ--nowiki-00000022-QINU`"'; LBL='"`UNIQ--nowiki-00000023-QINU`"'; UST={{#invoke:decodeEncode|encode|charset=^%z|s=[[{{UnstripNoWiki|#%i}}|%l]]}}; SUB={{#invoke:decodeEncode|encode|charset=^z|s=[[{{UnstripNoWiki|#math_'"`UNIQ--nowiki-00000022-QINU`"'}}|'"`UNIQ--nowiki-00000023-QINU`"']]}}; EXP=[[ #math_= 78''|'"`UNIQ--nowiki-00000023-QINU`"']];✶
[[
#math_= 78''|'"`UNIQ--nowiki-00000023-QINU`"']]
FMT='"`UNIQ--nowiki-00000025-QINU`"'; ID=math_'"`UNIQ--nowiki-00000026-QINU`"'; LBL='"`UNIQ--nowiki-00000027-QINU`"'; UST={{#invoke:string|replace|[[{{UnstripNoWiki|#%i}}|%l]]|ol|[q]|9|false}}; SUB={{#invoke:string|replace|[[{{UnstripNoWiki|#math_'"`UNIQ--nowiki-00000026-QINU`"'}}|'"`UNIQ--nowiki-00000027-QINU`"']]|ol|[q]|9|false}}; EXP=[[
#math_= 78''|'"`UNIQ--nowiki-00000027-QINU`"']];✶
[[
math_= 78|{{=}} 8'']] FMT='"`UNIQ--nowiki-00000029-QINU`"'; ID=math_'"`UNIQ--nowiki-0000002A-QINU`"'; LBL='"`UNIQ--nowiki-0000002B-QINU`"'; UST={{UnstripNoWiki|[[#%i|%l]]}}; SUB={{UnstripNoWiki|[[#math_'"`UNIQ--nowiki-0000002A-QINU`"'|'"`UNIQ--nowiki-0000002B-QINU`"']]}}; EXP=[[#math_= 8''|{{=}} 8'']];✶
{{=}} 8
FMT='"`UNIQ--nowiki-0000002D-QINU`"'; ID=math_'"`UNIQ--nowiki-0000002E-QINU`"'; LBL='"`UNIQ--nowiki-0000002F-QINU`"'; UST={{expand wikitext|{{UnstripNoWiki|[[#%i|%l]]}}}}; SUB={{expand wikitext|{{UnstripNoWiki|[[#math_'"`UNIQ--nowiki-0000002E-QINU`"'|'"`UNIQ--nowiki-0000002F-QINU`"']]}}}}; EXP=[[#math_= 8''|= 8'']];✶
= 8
FMT='"`UNIQ--nowiki-00000031-QINU`"'; ID=math_'"`UNIQ--nowiki-00000032-QINU`"'; LBL='"`UNIQ--nowiki-00000033-QINU`"'; UST=[[{{UnstripNoWiki|#%i}}|%l]]; SUB=[[{{UnstripNoWiki|#math_'"`UNIQ--nowiki-00000032-QINU`"'}}|'"`UNIQ--nowiki-00000033-QINU`"']]; EXP=[[
#math_{{=}} 8''|'"`UNIQ--nowiki-00000033-QINU`"']];✶
[[
math_{{=}} 8|{{=}} 8'']] FMT=[[#%i|%l]]; ID=someFrag; LBL='"`UNIQ--nowiki-00000035-QINU`"'; UST=[[#%i|%l]]; SUB=[[#someFrag|'"`UNIQ--nowiki-00000035-QINU`"']]; EXP=[[#someFrag|'"`UNIQ--nowiki-00000035-QINU`"']];✶
{{=}} 3''
= 3'' [[#abc|top]]
FMT='"`UNIQ--nowiki-00000037-QINU`"'; ID=foo; LBL=bar; UST=%Lnowiki%G{{=}} 3'' [[#abc|top]]%L/nowiki%G; SUB=<nowiki>{{=}} 3'' [[#abc|top]]</nowiki>; EXP='"`UNIQ--nowiki-00000038-QINU`"';✶
{{=}} 3'' [[#abc|top]]
FMT='"`UNIQ--nowiki-0000003A-QINU`"'; ID=foo; LBL=bar; UST={{=}}; SUB={{=}}; EXP==;✶
=
FMT='"`UNIQ--nowiki-0000003C-QINU`"'; ID=foo; LBL=bar; UST=%Lb%GwXyZ%L/b%G; SUB=<b>wXyZ</b>; EXP=<b>wXyZ</b>;✶
wXyZ
FMT='"`UNIQ--nowiki-0000003E-QINU`"'; ID=foo; LBL=bar; UST=<b>wXyZ</b>; SUB=<b>wXyZ</b>; EXP=<b>wXyZ</b>;✶
<b>wXyZ</b>
FMT='"`UNIQ--nowiki-00000040-QINU`"'; ID=; LBL='"`UNIQ--nowiki-00000041-QINU`"'; UST={{#invoke:decodeEncode|encode|charset=%L%G" \'&{{=}}|s=%l}}; SUB={{#invoke:decodeEncode|encode|charset=<>" \'&{{=}}|s='"`UNIQ--nowiki-00000041-QINU`"'}}; EXP='"`UNIQ--nowiki-00000041-QINU`"';✶
'"`UNIQ--nowiki-00000041-QINU`"'
FMT='"`UNIQ--nowiki-00000043-QINU`"'; ID=; LBL==lt; UST={{#invoke:decodeEncode|encode|charset=%L%G" \'&{{=}}|s=%l}}; SUB={{#invoke:decodeEncode|encode|charset=<>" \'&{{=}}|s==lt}}; EXP==lt;✶
=lt
FMT='"`UNIQ--nowiki-00000045-QINU`"'; ID=; LBL==lt; UST={{#invoke:decodeEncode|encode|charset=<>" \'&{{=}}|s=%l}}; SUB={{#invoke:decodeEncode|encode|charset=<>" \'&{{=}}|s==lt}}; EXP==lt;✶
=lt
FMT='"`UNIQ--nowiki-00000047-QINU`"'; ID=; LBL=3''; UST={{#invoke:decodeEncode|encode|s=%l}}; SUB={{#invoke:decodeEncode|encode|s=3''}}; EXP=3'';✶
3''
y
=
a
x
+
b
=
3
X
X
{\displaystyle y=ax+b=3XX}
FMT='"`UNIQ--nowiki-0000004B-QINU`"'; ID=math_3XX<nowiki>'</nowiki>; LBL=3XX<nowiki>'</nowiki>; UST=[[#%i|{{expand wikitext|{{#invoke:decodeEncode|decode|s=%l}}}}]]; SUB=[[#math_3XX<nowiki>'</nowiki>|{{expand wikitext|{{#invoke:decodeEncode|decode|s=3XX<nowiki>'</nowiki>}}}}]]; EXP=[[#math_3XX<nowiki>'</nowiki>|3XX'"`UNIQ--nowiki-0000004C-QINU`"']];✶
3XX'
y
=
a
x
+
b
{\displaystyle y=ax+b}
[[#math_5'|5']]
y
=
a
x
+
b
{\displaystyle y=ax+b}
5555'
y
=
a
x
+
b
{\displaystyle y=ax+b}
FMT=[[#%i|%l]]; ID=math_'"`UNIQ--nowiki-00000057-QINU`"'; LBL='"`UNIQ--nowiki-00000057-QINU`"'; UST=[[#%i|%l]]; SUB=[[#math_'"`UNIQ--nowiki-00000057-QINU`"'|'"`UNIQ--nowiki-00000057-QINU`"']]; EXP=[[#math_'"`UNIQ--nowiki-00000057-QINU`"'|'"`UNIQ--nowiki-00000057-QINU`"']];✶
[[#math_'"`UNIQ--nowiki-00000057-QINU`"'|'"`UNIQ--nowiki-00000057-QINU`"']]
y
=
a
x
+
b
{\displaystyle y=ax+b}
FMT=[[#%i|%l]]; ID=math_7''; LBL=7''; UST=[[#%i|%l]]; SUB=[[#math_7''|7'']]; EXP=[[#math_7''|7'']];✶
7''
e
c
{\displaystyle {\frac {e}{c}}}
FMT='"`UNIQ--nowiki-0000005F-QINU`"'; ID=math_4; LBL=4; UST='''[[#%i|%l]]'''%Lref%G{{cite web|url=https://gemini.google.com/app|title=Google Gemini}}%L/ref%G; SUB='''[[#math_4|4]]'''<ref>{{cite web|url=https://gemini.google.com/app|title=Google Gemini}}</ref>; EXP='''[[#math_4|4]]''''"`UNIQ--ref-00000060-QINU`"';✶
4 [ 1]
FMT='"`UNIQ--nowiki-00000062-QINU`"'; ID=ykk; LBL=land; UST=x{{((}}={{))}}y; %Lb%Gblah%L/b%G_%i_foo_%l_quax; SUB=x{{((}}={{))}}y; <b>blah</b>_ykk_foo_land_quax; EXP=x{{=}}y; <b>blah</b>_ykk_foo_land_quax;✶
x{{=}}y; blah _ykk_foo_land_quax
y
=
a
x
+
b
=
3
C
{\displaystyle y=ax+b=3C}
3C'
y
=
a
x
+
b
=
3
B
{\displaystyle y=ax+b=3B}
FMT='"`UNIQ--nowiki-0000006A-QINU`"'; ID=math_3B<nowiki>'</nowiki>; LBL=3B<nowiki>'</nowiki>; UST=[[#%i|{{UnstripNoWiki|{{#invoke:decodeEncode|decode|s=%l}}}}]]; SUB=[[#math_3B<nowiki>'</nowiki>|{{UnstripNoWiki|{{#invoke:decodeEncode|decode|s=3B<nowiki>'</nowiki>}}}}]]; EXP=[[#math_3B<nowiki>'</nowiki>|3B<nowiki>'</nowiki>]];✶
3B<nowiki>'</nowiki>
下面這段說明因這裡 提到「Recommendation is currently restricted to use inside TemplateStyles (phab:T360562, phab:T361934).」,所以就先不更新到NumBlk的說明頁面了。
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
18
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
28
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
38
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
48
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
58
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
68
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
78
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
88
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
98
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
108
v
=
s
t
{\displaystyle v={\frac {s}{t}}}
118
Transcluded categories [ 编辑 ] {{ 滾動 中直接叫用{{NumBlk }}的例子
F
net
=
F
external
−
F
friction
{\displaystyle F_{\text{net}}=F_{\text{external}}-F_{\text{friction}}}
(
1
)
{\displaystyle (1)}
}} 滾動 中直接叫用{{NumBlk }}的例子
y
=
a
x
+
b
{\displaystyle y=ax+b}
Eq. 3778
a
x
2
+
b
x
+
c
=
0
{\displaystyle ax^{2}+bx+c=0}
Eq. 3779
Ψ
(
x
1
,
x
2
)
=
U
(
x
1
)
V
(
x
2
)
{\displaystyle \Psi (x_{1},x_{2})=U(x_{1})V(x_{2})}
1780
Fe3+ + H2 O2 → Fe2+ + HOO• + H+ 2781
H
+
+
CO
3
2
−
⟶
HCO
3
−
{\displaystyle {\ce {H+ + CO3^2- -> HCO3^-}}}
3782
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
3.5783
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
1784
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
13.7785
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
1.2786
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
3.5787
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
<3.5788a>
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
<3.5788b>
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
< 3.5788c>
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
<3.5788d>
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
[ 3.5789]
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
[ 3.5790]
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
[3.5791]
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
[ 3.5792]
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
<Big>(3.5794a) </Big>
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
( 3.5794b)
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
( 3.5795)
y
=
a
x
+
b
{\displaystyle y=ax+b}
Eq. 3830
y
=
a
x
+
b
{\displaystyle y=ax+b}
Eq. 3831
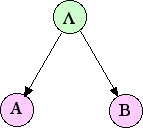
Fig.1: Bayesian Network representation of Eq.(6) Fig.1: Bayesian Network representation of Eq.(6)
P
(
a
,
b
,
λ
)
=
P
(
a
|
λ
)
P
(
b
|
λ
)
P
(
λ
)
{\displaystyle P(a,b,\lambda )=P(a|\lambda )P(b|\lambda )P(\lambda )\,}
Eq.(6832)
PCl
5
⏟
(
1
)
→
Me
2
NH
[
(
Me
2
N
)
3
P
⊕
−
Cl
⋅
C
⊖
l
]
⏟
(
2
)
→
2.
NaBF
4
1.
NH
3
(
Me
2
N
)
3
P
⊕
−
NH
2
⋅
B
⊖
F
4
⏟
(
3
)
{\displaystyle {\begin{matrix}{}\\\underbrace {\ce {PCl5}} _{(1)}\ {\ce {->[{\ce {Me2NH}}]}}\underbrace {\left[{\ce {(Me2N)3{\overset {\oplus }{P}}-Cl.{\overset {\ominus }{C}}l}}\right]} _{(2)}\ {\ce {->[1.\ {\ce {NH3}}][2.\ {\ce {NaBF4}}]}}\ \underbrace {\ce {(Me2N)3{\overset {\oplus }{P}}-NH2.{\overset {\ominus }{B}}F4}} _{(3)}\\{}\end{matrix}}}
[ A1 ]
(
Me
2
N
)
3
P
⊕
−
NH
2
⋅
B
⊖
F
4
⏟
(
3
)
→
KOMe
(
Me
2
N
)
3
P
=
NH
⏟
(
4
)
{\displaystyle \underbrace {\ce {(Me2N)3{\overset {\oplus }{P}}-NH2.{\overset {\ominus }{B}}F4}} _{(3)}\ {\ce {->[{\ce {KOMe}}]}}\ \underbrace {\ce {(Me2N)3P=NH}} _{(4)}}
[ A2 ]
[ A ]
2=foo; 1=blah;
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
2=math_101; 1=101;
a
(
t
)
=
d
d
t
v
(
t
)
{\displaystyle \mathbf {a} (t)={\frac {d}{dt}}\mathbf {v} (t)}
{{使用者:Justin545/沙盒/ex3|math_102|102}}
PCl
5
⏟
(
1
)
→
t
-
Bu
−
NH
3
⊕
⋅
Cl
⊖
t
-
Bu
−
N
=
PCl
3
⏟
(
5
)
{\displaystyle \underbrace {\ce {PCl5}} _{(1)}\ {\ce {->[t{\text{-}}{\ce {Bu-{\overset {\oplus }{NH3}}.{\overset {\ominus }{Cl}}}}]}}\ \underbrace {t{\text{-}}{\ce {Bu-N=PCl3}}} _{(5)}}
175
#not-exist
y
=
a
x
+
b
{\displaystyle y=ax+b}
16
y
=
a
x
+
b
{\displaystyle y=ax+b}
5
y
=
a
x
+
b
{\displaystyle y=ax+b}
49
y
=
a
x
+
b
{\displaystyle y=ax+b}
90
y
=
a
x
+
b
{\displaystyle y=ax+b}
377
y
=
a
x
+
b
{\displaystyle y=ax+b}
8
y
=
a
x
+
b
{\displaystyle y=ax+b}
8
y
=
a
x
+
b
{\displaystyle y=ax+b}
(8 )
y
=
a
x
+
b
{\displaystyle y=ax+b}
(8 )
{{subst:#ifexpr:5 > 0|表达式错误:无法识别标点符号“{”。 |1}}
{{subst:#ifexpr:5 > 0|表达式错误:无法识别标点符号“{”。 |1}}
{{subst:#ifexpr:5 > 0|表达式错误:无法识别标点符号“{”。 |1}}
{{subst:#ifexpr:5 > 0|表达式错误:无法识别标点符号“{”。 |1}}
{{subst:#ifexpr:5 > 0|表达式错误:无法识别标点符号“{”。 |1}}
{{subst:#ifexpr:5 > 0|表达式错误:无法识别标点符号“{”。 |1}}
區塊(73 16 5 49 90 377 )!
終結 完結 殲滅 消滅 消除 斷絕 阻絕 杜絕 瓦解 解放 禁
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1-o
--- 0.00108(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.5-o
--- 0.00096000000000002(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.6-o
--- 0.00198(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.7-o
--- 0.00106(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.8-o
--- 0.00087999999999999(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.9-o
--- 0.00089999999999998(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.91-o
--- 0.00094(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.92-o
--- 0.00094(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.93-o
--- 0.00086(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.931-o2
--- 0.00114(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.932-o2
--- 0.0012(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.933-o2
--- 0.00118(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.934-o2
--- 0.00108(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.935-o2
--- 0.00112(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.936-o2
--- 0.00112(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.937-o2
--- 0.00114(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.938-o2
--- 0.00212(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1.939-o2
--- 0.00124(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
{Def.1.940-o2f }
--- 0.00174(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
{Def.1.941-o2f }
--- 0.00174(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
{Def.1.942-o2f }
--- 0.00166(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
{Def.1.943-o2f }
--- 0.00172(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
{Def.1.944-o2f }
--- 0.00164(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
{Def.1.945-o2f }
--- 0.00174(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1-ex5
--- 0.00402(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.2-ex5
--- 0.00188(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.3-ex5
--- 0.00286(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.4-ex5
--- 0.00196(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.5-ex5
--- 0.0019(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.6-ex5
--- 0.00184(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.7-ex5
--- 0.00188(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.8-ex5
--- 0.00186(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.9-ex5
--- 0.00196(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.10-ex5
--- 0.0019(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.1-ex4
--- 0.00136(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.2-ex4
--- 0.00232(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.3-ex4
--- 0.00134(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.4-ex4
--- 0.00134(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.5-ex4
--- 0.00136(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.6-ex4
--- 0.00146(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.7-ex4
--- 0.00132(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.8-ex4
--- 0.00132(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.9-ex4
--- 0.00136(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
Def.10-ex4
--- 0.00132(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
(Def.2-s)
--- 0.00334(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
(Def.3-s)
--- 0.00096000000000002(second)
f
′
(
x
)
=
lim
h
→
0
f
(
x
+
h
)
−
f
(
x
)
h
{\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}
(Def.4-s)
--- 0.00094(second)
y
=
a
x
+
b
{\displaystyle y=ax+b}
(5-s)
--- 0.00094(second)
H
+
+
CO
3
2
−
⟶
HCO
3
−
{\displaystyle {\ce {H+ + CO3^2- -> HCO3^-}}}
(6-s)
--- 0.00087999999999999(second)
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x}
(7-s)
--- 0.002(second)
(
∂
z
∂
x
(
x
,
y
)
,
∂
z
∂
y
(
x
,
y
)
,
−
1
)
{\displaystyle \left({\frac {\partial z}{\partial x}}(x,y),{\frac {\partial z}{\partial y}}(x,y),-1\right)}
(8-s)
--- 0.00094(second)
y
=
a
x
+
b
+
10
{\displaystyle y=ax+b+10}
y
=
a
x
+
b
+
11
{\displaystyle y=ax+b+11}
y
=
a
x
+
b
+
1
{\displaystyle y=ax+b+1}
y
=
a
x
+
b
+
2
{\displaystyle y=ax+b+2}
y
=
a
x
+
b
+
3
{\displaystyle y=ax+b+3}
y
=
a
x
+
b
+
4
{\displaystyle y=ax+b+4}
y
=
a
x
+
b
+
5
{\displaystyle y=ax+b+5}
db6d77809cf77e2d00a078cd68e9f223
y
=
a
x
+
b
{\displaystyle y=ax+b}
13579
eeb14ff26fc101c7a74e492fb57c5d2e
y
=
a
x
+
b
+
7
{\displaystyle y=ax+b+7}
y
=
a
x
+
b
+
8
{\displaystyle y=ax+b+8}
y
=
a
x
+
b
+
9
{\displaystyle y=ax+b+9}
y
=
a
x
+
b
{\displaystyle y=ax+b}
41
y
=
a
x
+
b
{\displaystyle y=ax+b}
42
y
=
a
x
+
b
{\displaystyle y=ax+b}
43
y
=
a
x
+
b
{\displaystyle y=ax+b}
51
y
=
a
x
+
b
{\displaystyle y=ax+b}
52
y
=
a
x
+
b
{\displaystyle y=ax+b}
53
y
=
a
x
+
b
{\displaystyle y=ax+b}
61
y
=
a
x
+
b
{\displaystyle y=ax+b}
62
y
=
a
x
+
b
{\displaystyle y=ax+b}
63
Indentation comparisons [ 编辑 ]
y
=
a
x
+
b
+
70
{\displaystyle y=ax+b+70}
y
=
a
x
+
b
{\displaystyle y=ax+b}
70.5
y
=
a
x
+
b
+
71
{\displaystyle y=ax+b+71}
y
=
a
x
+
b
{\displaystyle y=ax+b}
71.5
y
=
a
x
+
b
+
72
{\displaystyle y=ax+b+72}
y
=
a
x
+
b
{\displaystyle y=ax+b}
72.5
y
=
a
x
+
b
+
73
{\displaystyle y=ax+b+73}
y
=
a
x
+
b
{\displaystyle y=ax+b}
73.5
y
=
a
x
+
b
+
79
{\displaystyle y=ax+b+79}
y
=
a
x
+
b
{\displaystyle y=ax+b}
79.5
When content of the blocks and block numbers are far apart [ 编辑 ]
Markup
< div style = "line-height:0;" >
{{ NumBlk | 1 = :| 2 = < math > a^ 2 + b^ 2 = (a + b i) (a - b i)</ math >| 3 = 1}}
{{ NumBlk | 1 = :| 2 = < math > a^ 2 - b^ 2 = (a + b) (a - b)</ math >| 3 = 2}}
{{ NumBlk | 1 = :| 2 = < math > e^{ i x} = \cos x + i \sin x</ math >| 3 = 3}}
{{ NumBlk | 1 = :| 2 = < math > \sin ^ 2 \theta + \cos ^ 2 \theta = 1</ math >| 3 = 4}}
{{ NumBlk | 1 = :| 2 = < math > \sin (2 \theta ) = 2 \sin \theta \cos \theta </ math >| 3 = 5}}
</ div >
Renders as
a
2
+
b
2
=
(
a
+
b
i
)
(
a
−
b
i
)
{\displaystyle a^{2}+b^{2}=(a+bi)(a-bi)}
1
a
2
−
b
2
=
(
a
+
b
)
(
a
−
b
)
{\displaystyle a^{2}-b^{2}=(a+b)(a-b)}
2
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x}
3
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
4
sin
(
2
θ
)
=
2
sin
θ
cos
θ
{\displaystyle \sin(2\theta )=2\sin \theta \cos \theta }
5
Markup
< div style = "line-height:0;" >
{{ NumBlk | 1 = :| 2 = < math > a^ 2 + b^ 2 = (a + b i) (a - b i)</ math >| 3 = 1| LnSty = 0.37ex dotted Gainsboro}}
{{ NumBlk | 1 = :| 2 = < math > a^ 2 - b^ 2 = (a + b) (a - b)</ math >| 3 = 2| LnSty = 0.37ex dotted Gainsboro}}
{{ NumBlk | 1 = :| 2 = < math > e^{ i x} = \cos x + i \sin x</ math >| 3 = 3| LnSty = 0.37ex dotted Gainsboro}}
{{ NumBlk | 1 = :| 2 = < math > \sin ^ 2 \theta + \cos ^ 2 \theta = 1</ math >| 3 = 4| LnSty = 0.37ex dotted Gainsboro}}
{{ NumBlk | 1 = :| 2 = < math > \sin (2 \theta ) = 2 \sin \theta \cos \theta </ math >| 3 = 5| LnSty = 0.37ex dotted Gainsboro}}
</ div >
Renders as
a
2
+
b
2
=
(
a
+
b
i
)
(
a
−
b
i
)
{\displaystyle a^{2}+b^{2}=(a+bi)(a-bi)}
1
a
2
−
b
2
=
(
a
+
b
)
(
a
−
b
)
{\displaystyle a^{2}-b^{2}=(a+b)(a-b)}
2
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x}
3
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
4
sin
(
2
θ
)
=
2
sin
θ
cos
θ
{\displaystyle \sin(2\theta )=2\sin \theta \cos \theta }
5
Markup
< div style = "line-height:0;" >
{{ NumBlk | 1 = :| 2 = < math > a^ 2 + b^ 2 = (a + b i) (a - b i)</ math >| 3 = 1| LnSty = 0.37ex dotted Gainsboro}}
{{ NumBlk | 1 = :| 2 = < math > a^ 2 - b^ 2 = (a + b) (a - b)</ math >| 3 = 2| LnSty = 0.37ex none Gainsboro}}
{{ NumBlk | 1 = :| 2 = < math > e^{ i x} = \cos x + i \sin x</ math >| 3 = 3| LnSty = 0.37ex dotted Gainsboro}}
{{ NumBlk | 1 = :| 2 = < math > \sin ^ 2 \theta + \cos ^ 2 \theta = 1</ math >| 3 = 4| LnSty = 0.37ex none Gainsboro}}
{{ NumBlk | 1 = :| 2 = < math > \sin (2 \theta ) = 2 \sin \theta \cos \theta </ math >| 3 = 5| LnSty = 0.37ex dotted Gainsboro}}
</ div >
Renders as
a
2
+
b
2
=
(
a
+
b
i
)
(
a
−
b
i
)
{\displaystyle a^{2}+b^{2}=(a+bi)(a-bi)}
1
a
2
−
b
2
=
(
a
+
b
)
(
a
−
b
)
{\displaystyle a^{2}-b^{2}=(a+b)(a-b)}
2
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x}
3
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
4
sin
(
2
θ
)
=
2
sin
θ
cos
θ
{\displaystyle \sin(2\theta )=2\sin \theta \cos \theta }
5
Markup
< div style = "line-height:0;" >
< div style = "background-color: Beige;" >
{{ NumBlk | 1 = :| 2 = < math > a^ 2 + b^ 2 = (a + b i) (a - b i)</ math >| 3 = 1}}
</ div > < div style = "background-color: none;" >
{{ NumBlk | 1 = :| 2 = < math > a^ 2 - b^ 2 = (a + b) (a - b)</ math >| 3 = 2}}
</ div > < div style = "background-color: Beige;" >
{{ NumBlk | 1 = :| 2 = < math > e^{ i x} = \cos x + i \sin x</ math >| 3 = 3}}
</ div > < div style = "background-color: none;" >
{{ NumBlk | 1 = :| 2 = < math > \sin ^ 2 \theta + \cos ^ 2 \theta = 1</ math >| 3 = 4}}
</ div > < div style = "background-color: Beige;" >
{{ NumBlk | 1 = :| 2 = < math > \sin (2 \theta ) = 2 \sin \theta \cos \theta </ math >| 3 = 5}}
</ div >
</ div >
Renders as
a
2
+
b
2
=
(
a
+
b
i
)
(
a
−
b
i
)
{\displaystyle a^{2}+b^{2}=(a+bi)(a-bi)}
1
a
2
−
b
2
=
(
a
+
b
)
(
a
−
b
)
{\displaystyle a^{2}-b^{2}=(a+b)(a-b)}
2
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x}
3
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}
4
sin
(
2
θ
)
=
2
sin
θ
cos
θ
{\displaystyle \sin(2\theta )=2\sin \theta \cos \theta }
5
Proof of hypothetical syllogism by constructive dilemma [ 编辑 ]
(
p
→
q
)
↔
(
¬
q
→
¬
p
)
{\displaystyle (p\rightarrow q)\leftrightarrow (\neg q\rightarrow \neg p)}
/ / Lemma: Logical equivalences involving conditional statements B
p
∧
⊤
↔
p
{\displaystyle p\land \top \leftrightarrow p}
/ / Lemma: Identity laws A
p
∨
¬
p
↔
⊤
{\displaystyle p\lor \neg p\leftrightarrow \top }
/ / Lemma: Negation laws A
[
(
P
→
Q
)
∧
(
R
→
S
)
∧
(
P
∨
R
)
]
→
(
Q
∨
S
)
{\displaystyle [(P\rightarrow Q)\land (R\rightarrow S)\land (P\lor R)]\rightarrow (Q\lor S)}
/ / Lemma: Constructive dilemma
(
p
→
q
)
↔
(
¬
p
∨
q
)
{\displaystyle (p\rightarrow q)\leftrightarrow (\neg p\lor q)}
/ / Lemma: Logical equivalences involving conditional statements A
(
p
→
q
)
∧
(
q
→
r
)
{\displaystyle (p\rightarrow q)\land (q\rightarrow r)}
.1 / / premise
(
p
→
q
)
↔
(
¬
q
→
¬
p
)
|
p
:
p
q
:
q
{\displaystyle (p\rightarrow q)\leftrightarrow (\neg q\rightarrow \neg p)\;\left|\;{\begin{array}{l}p:p\\q:q\end{array}}\right.}
.11 / .1 / Logical equivalences involving conditional statements B
(
p
→
q
)
↔
(
¬
q
→
¬
p
)
{\displaystyle (p\rightarrow q)\leftrightarrow (\neg q\rightarrow \neg p)}
.12 / .11
(
¬
q
→
¬
p
)
∧
(
q
→
r
)
{\displaystyle (\neg q\rightarrow \neg p)\land (q\rightarrow r)}
.13 / .1 .12
p
∧
⊤
↔
p
|
p
:
(
¬
q
→
¬
p
)
∧
(
q
→
r
)
{\displaystyle p\land \top \leftrightarrow p\;|\;p:(\neg q\rightarrow \neg p)\land (q\rightarrow r)}
.14 / .13 / Identity laws A
[
(
¬
q
→
¬
p
)
∧
(
q
→
r
)
]
∧
⊤
↔
(
¬
q
→
¬
p
)
∧
(
q
→
r
)
{\displaystyle [(\neg q\rightarrow \neg p)\land (q\rightarrow r)]\land \top \leftrightarrow (\neg q\rightarrow \neg p)\land (q\rightarrow r)}
.15 / .14
(
¬
q
→
¬
p
)
∧
(
q
→
r
)
∧
⊤
↔
(
¬
q
→
¬
p
)
∧
(
q
→
r
)
{\displaystyle (\neg q\rightarrow \neg p)\land (q\rightarrow r)\land \top \leftrightarrow (\neg q\rightarrow \neg p)\land (q\rightarrow r)}
.16 / .15
(
¬
q
→
¬
p
)
∧
(
q
→
r
)
∧
⊤
{\displaystyle (\neg q\rightarrow \neg p)\land (q\rightarrow r)\land \top }
.17 / .13 .16
(
q
→
r
)
∧
(
¬
q
→
¬
p
)
∧
⊤
{\displaystyle (q\rightarrow r)\land (\neg q\rightarrow \neg p)\land \top }
.18 / .17
p
∨
¬
p
↔
⊤
|
p
:
q
{\displaystyle p\lor \neg p\leftrightarrow \top \;|\;p:q}
.19 / .18 / Negation laws A
q
∨
¬
q
↔
⊤
{\displaystyle q\lor \neg q\leftrightarrow \top }
.2 / .19
(
q
→
r
)
∧
(
¬
q
→
¬
p
)
∧
(
q
∨
¬
q
)
{\displaystyle (q\rightarrow r)\land (\neg q\rightarrow \neg p)\land (q\lor \neg q)}
.21 / .18 .2
[
(
P
→
Q
)
∧
(
R
→
S
)
∧
(
P
∨
R
)
]
→
(
Q
∨
S
)
|
P
:
q
Q
:
r
R
:
¬
q
S
:
¬
p
{\displaystyle [(P\rightarrow Q)\land (R\rightarrow S)\land (P\lor R)]\rightarrow (Q\lor S)\;\left|\;{\begin{array}{l}P:q\\Q:r\\R:\neg q\\S:\neg p\end{array}}\right.}
.22 / .21 / Constructive dilemma
[
(
q
→
r
)
∧
(
¬
q
→
¬
p
)
∧
(
q
∨
¬
q
)
]
→
(
r
∨
¬
p
)
{\displaystyle [(q\rightarrow r)\land (\neg q\rightarrow \neg p)\land (q\lor \neg q)]\rightarrow (r\lor \neg p)}
.23 / .22
[
(
q
→
r
)
∧
(
¬
q
→
¬
p
)
∧
(
q
∨
¬
q
)
]
→
(
¬
p
∨
r
)
{\displaystyle [(q\rightarrow r)\land (\neg q\rightarrow \neg p)\land (q\lor \neg q)]\rightarrow (\neg p\lor r)}
.24 / .23
(
p
→
q
)
↔
(
¬
p
∨
q
)
|
p
:
p
q
:
r
{\displaystyle (p\rightarrow q)\leftrightarrow (\neg p\lor q)\;\left|\;{\begin{array}{l}p:p\\q:r\end{array}}\right.}
.25 / .24 / Logical equivalences involving conditional statements A
(
p
→
r
)
↔
(
¬
p
∨
r
)
{\displaystyle (p\rightarrow r)\leftrightarrow (\neg p\lor r)}
.26 / .25
[
(
q
→
r
)
∧
(
¬
q
→
¬
p
)
∧
(
q
∨
¬
q
)
]
→
(
p
→
r
)
{\displaystyle [(q\rightarrow r)\land (\neg q\rightarrow \neg p)\land (q\lor \neg q)]\rightarrow (p\rightarrow r)}
.27 / .24 .26
[
(
q
→
r
)
∧
(
¬
q
→
¬
p
)
∧
⊤
]
→
(
p
→
r
)
{\displaystyle [(q\rightarrow r)\land (\neg q\rightarrow \neg p)\land \top ]\rightarrow (p\rightarrow r)}
.28 / .2 .27
[
(
¬
q
→
¬
p
)
∧
(
q
→
r
)
∧
⊤
]
→
(
p
→
r
)
{\displaystyle [(\neg q\rightarrow \neg p)\land (q\rightarrow r)\land \top ]\rightarrow (p\rightarrow r)}
.29 / .28
[
(
¬
q
→
¬
p
)
∧
(
q
→
r
)
]
→
(
p
→
r
)
{\displaystyle [(\neg q\rightarrow \neg p)\land (q\rightarrow r)]\rightarrow (p\rightarrow r)}
.3 / .16 .29
[
(
p
→
q
)
∧
(
q
→
r
)
]
→
(
p
→
r
)
{\displaystyle [(p\rightarrow q)\land (q\rightarrow r)]\rightarrow (p\rightarrow r)}
.31 / .12 .3 / conclusion
^ Google Gemini .
















![{\displaystyle {\begin{matrix}{}\\\underbrace {\ce {PCl5}} _{(1)}\ {\ce {->[{\ce {Me2NH}}]}}\underbrace {\left[{\ce {(Me2N)3{\overset {\oplus }{P}}-Cl.{\overset {\ominus }{C}}l}}\right]} _{(2)}\ {\ce {->[1.\ {\ce {NH3}}][2.\ {\ce {NaBF4}}]}}\ \underbrace {\ce {(Me2N)3{\overset {\oplus }{P}}-NH2.{\overset {\ominus }{B}}F4}} _{(3)}\\{}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/934831033e3d3a948ab3ad1435b54d3955156102)
![{\displaystyle \underbrace {\ce {(Me2N)3{\overset {\oplus }{P}}-NH2.{\overset {\ominus }{B}}F4}} _{(3)}\ {\ce {->[{\ce {KOMe}}]}}\ \underbrace {\ce {(Me2N)3P=NH}} _{(4)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f770d8ef6ebd14dd05f206b5a5834c39af323aaf)



![{\displaystyle \underbrace {\ce {PCl5}} _{(1)}\ {\ce {->[t{\text{-}}{\ce {Bu-{\overset {\oplus }{NH3}}.{\overset {\ominus }{Cl}}}}]}}\ \underbrace {t{\text{-}}{\ce {Bu-N=PCl3}}} _{(5)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9273434d7f39954c83fec9f0e179ee064ad1afe)




























![{\displaystyle [(P\rightarrow Q)\land (R\rightarrow S)\land (P\lor R)]\rightarrow (Q\lor S)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad4b1251ab100a709417bbcff090b8f34db6d71c)





![{\displaystyle [(\neg q\rightarrow \neg p)\land (q\rightarrow r)]\land \top \leftrightarrow (\neg q\rightarrow \neg p)\land (q\rightarrow r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44f0c9e0d9e8756fe070e60bee723cd012413454)






![{\displaystyle [(P\rightarrow Q)\land (R\rightarrow S)\land (P\lor R)]\rightarrow (Q\lor S)\;\left|\;{\begin{array}{l}P:q\\Q:r\\R:\neg q\\S:\neg p\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4579ea1404ac230c904bddaa6f9e297a34362a8)
![{\displaystyle [(q\rightarrow r)\land (\neg q\rightarrow \neg p)\land (q\lor \neg q)]\rightarrow (r\lor \neg p)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0486c8929558f05962e6ff52d7197b65fb1f2d50)
![{\displaystyle [(q\rightarrow r)\land (\neg q\rightarrow \neg p)\land (q\lor \neg q)]\rightarrow (\neg p\lor r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40123349b2b0adf3f69b8a1dfe7809cc0bb252c7)


![{\displaystyle [(q\rightarrow r)\land (\neg q\rightarrow \neg p)\land (q\lor \neg q)]\rightarrow (p\rightarrow r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5761277022739bed36af7d3876287ebe06b474cf)
![{\displaystyle [(q\rightarrow r)\land (\neg q\rightarrow \neg p)\land \top ]\rightarrow (p\rightarrow r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34a57292d02f17bc725c648728f6cbe3168687c0)
![{\displaystyle [(\neg q\rightarrow \neg p)\land (q\rightarrow r)\land \top ]\rightarrow (p\rightarrow r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29c40828e033bf3e4cd7711423f23c9a02f430f6)
![{\displaystyle [(\neg q\rightarrow \neg p)\land (q\rightarrow r)]\rightarrow (p\rightarrow r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2f7ab5d2621107dbdd3fb8e219ebfe1de39251e)
![{\displaystyle [(p\rightarrow q)\land (q\rightarrow r)]\rightarrow (p\rightarrow r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/935a502500361b244f9e59056f5d9839cd20d67a)