圆偏振

对于一个行进的圆偏振电磁波，其電場矢量的旋转方向取决于观察者的视角。如果从波源的角度定义，此波为右旋/顺时针圆偏振；如果从接收者的角度定义，则此波为左旋/逆时针圆偏振。

在电动力学中，电磁波的圆偏振是一种偏振状态，其中波的电磁场在每个点上具有恒定的幅度，并在垂直于波传播方向的平面内以恒定速率旋转。

在电动力学中，电场的强度和方向由其电场矢量定义。对于圆偏振波，电场矢量的尖端在空间中的某一点上，随着光在时间和空间中的传播，与光的相位相关。在任何时刻，波的电场矢量都指向沿传播方向的一个螺旋线上的某一点。圆偏振波可以以两种可能的旋转方向进行旋转：右旋圆偏振（Right-Handed Circular Polarization, RHCP），即电场矢量相对于传播方向以右手螺旋方式旋转；以及左旋圆偏振（Left-Handed Circular Polarization, LHCP），即电场矢量以左手螺旋方式旋转。

圆偏振是椭圆偏振的一种极限情况，而另一种特殊情况是更容易理解的线性偏振。这三个术语均由奥古斯丁·菲涅耳创造，并于1822年12月9日在法国科学院的一篇论文中首次提出。菲涅耳早在1821年就首次描述了圆偏振的情况，但当时尚未命名。

偏振现象的产生是由于光表现为一种二维横波的结果。

当两个正交的电场分量矢量大小相等且相位差恰好为90°（即四分之一波长）时，就会产生圆偏振。

特征

右旋/逆时针圆偏振光可以通过使用组件或未使用组件的方式展示。如果从波源而非接收者的视角定义，这种光将被视为顺时针圆偏振。需要注意的是，圆偏振的旋向性（左旋或右旋）与波源或接收者的观察视角无关，旋向性本身是光的一种固有特性。

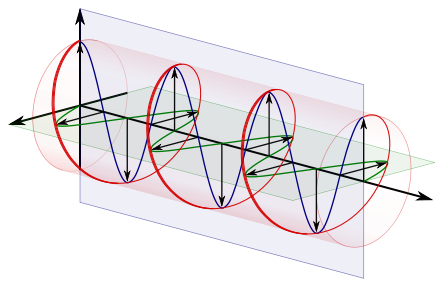
在圆偏振电磁波中，单个电场矢量及其合成矢量的大小保持不变，而相位角则不断变化。由于这是一种平面波，每个矢量代表了垂直于光轴的整个平面上电场的大小和方向。具体来说，对于这种圆偏振平面波，这些矢量表明电场在平面与平面之间具有恒定的强度，而其方向则稳定地旋转。可以参考平面波文章中的这两幅图像，以更好地理解这种动态特性。如果从接收者的视角观察，这种光被认为是右旋/顺时针圆偏振。由于这是一种電磁波，每个電場矢量都有一个对应的（但未图示的）磁場矢量，该磁场矢量与电场矢量成直角，并且大小与其成正比。因此，如果显示出来，磁场矢量将描绘出第二条螺旋线。

圆偏振经常在光学领域中出现，因此在本节中，电磁波将简称为光。

理解圆偏振的本质及其与其他偏振关系的一种常见方法是将电场视为被分解为两个相互垂直的分量。垂直分量及其对应的平面用蓝色表示，而水平分量及其对应的平面用绿色表示。注意，水平分量（相对于传播方向向右）比垂直分量领先四分之一波长，即90°的相位差。正是这种正交相位关系形成了螺旋线，并导致垂直分量最大值的点与水平分量为零的点对应，反之亦然。这种对齐的结果是选择了一些矢量，这些矢量与螺旋线完全匹配，并恰好对应于垂直和水平分量的最大值。

为了理解这种正交相位差如何对应于一个在保持恒定幅度的同时旋转的电场，可以想象一个点沿顺时针方向在圆上运动。考虑该点相对于圆心的垂直和水平位移如何随时间正弦变化，并且两者之间存在四分之一周期的相位差。位移被称为相差四分之一周期，因为水平最大位移（向左）比垂直最大位移提前四分之一周期达到。现在再次参考图示，想象刚刚描述的圆心沿轴线从前往后移动。这个旋转的点将描绘出一条螺旋线，其中向左的位移领先于垂直位移。正如旋转点的水平和垂直位移在时间上相差四分之一周期，电场的水平和垂直分量在空间上也相差四分之一波长。

左旋/逆时针圆偏振光可以通过使用组件或未使用组件的方式展示。如果从波源而非接收者的视角定义，这种光将被视为右旋/顺时针圆偏振。

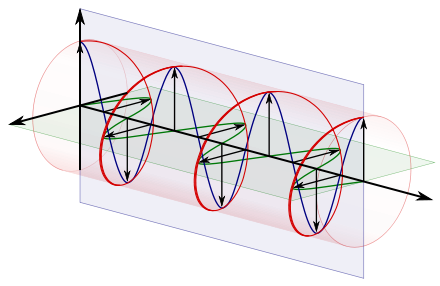
接下来的图示展示了从接收者视角观察到的左旋/逆时针圆偏振光。由于它是左旋的，相对于传播方向向右的水平分量现在比垂直分量滞后四分之一波长，而不是领先。

旋向性反转

波片

要将圆偏振光转换为另一种旋向性，可以使用半波片。半波片会将光的某一线性分量相对于其正交线性分量移动半个波长。

反射

在法向入射（垂直入射）的情况下，偏振光的旋向性在表面反射后会反转。在这种反射中，反射光的偏振平面的旋转方向与入射场相同。然而，由于传播方向现在相反，对于入射光束而言的“右旋”旋转方向，在反向传播时变为“左旋”，反之亦然。除了旋向性反转外，偏振的椭圆度也会保持不变（除非反射表面是双折射表面）。

需要注意的是，这一原理仅严格适用于法向入射的光。例如，从电介质表面以掠射角（超过布儒斯特角的角度）反射的右旋圆偏振光仍然会保持右旋，但会变为椭圆偏振。在非法向入射的情况下，金属表面反射的光通常也会改变其椭圆度。这些情况可以通过将入射的圆偏振（或其他偏振）分解为平行和垂直于入射平面的线性偏振分量（通常分别称为p和s分量）来解决。通过应用菲涅尔反射系数，可以找到p和s线性偏振分量的反射光，而这两个线性偏振分量的菲涅耳系数通常是不同的。只有在法向入射的特殊情况下，p和s分量之间没有区别，菲涅尔系数相同，从而导致上述特性。

一组包含三张幻灯片的图片，展示了佩戴和未佩戴MasterImage 3D圆偏振电影眼镜下的几只已死亡的欧洲玫瑰鞘虫（Cetonia aurata）。这些甲虫的闪亮绿色来自左偏振光。需要注意的是，在没有眼镜的情况下，甲虫及其图像都具有闪亮的颜色。右偏振器去除了甲虫的颜色，但保留了图像的颜色。左偏振器则相反，显示出反射光的手性反转。

转换为线性偏振

圆偏振光可以通过透过四分之一波片转化为线性偏振光。当线性偏振光通过四分之一波片，并且波片的光轴与其偏振轴成45°角时，光将被转换为圆偏振光。事实上，这种方法是实际中最常用的产生圆偏振光的方式。需要注意的是，当线性偏振光以其他角度通过四分之一波片时，通常会产生椭圆偏振光。

手性反转

这是一个从波源角度定义的右旋/顺时针圆偏振波。如果从接收者角度定义，该波将被视为左旋/逆时针圆偏振波。

这是一个从波源角度定义的左旋/逆时针圆偏振波。如果从接收者角度定义，该波将被视为右旋/顺时针圆偏振波。

圆偏振可以根据电场矢量的旋转方向被称为右旋或左旋，以及顺时针或逆时针。然而，历史上存在两种对立的定义惯例，这可能导致混淆。

从波源的角度定义

在这种惯例中，偏振是从波源的角度定义的。使用这种惯例时，左旋或右旋的确定方法是将左手或右手的拇指指向波源的反方向（即波的传播方向），并将手指的卷曲方向与电场在空间中某一点的时间旋转方向匹配。当确定波是顺时针还是逆时针圆偏振时，同样从波源的角度观察，背向波源并看向波的传播方向，观察电场的时间旋转方向。

根据这种惯例，左旋圆偏振波的电场矢量可以表示为：$\left(E_{x},\,E_{y},\,E_{z}\right)\propto \left(\cos {\frac {2\pi }{\lambda }}\left(ct-z\right),\,-\sin {\frac {2\pi }{\lambda }}\left(ct-z\right),\,0\right).$

例如，参考第一个动画中的圆偏振波。根据这种惯例，该波被定义为右旋，因为当右拇指指向波的传播方向时，手指的卷曲方向与电场的时间旋转方向一致。它也被认为是顺时针圆偏振，因为从波源的角度看，沿着波的传播方向观察，电场是顺时针旋转的。第二个动画则是根据同一惯例定义的左旋或逆时针光。

这种惯例符合电气电子工程师学会的标准，因此在工程领域被广泛使用。

量子物理学家也使用这种旋向性惯例，因为它与粒子自旋的旋向性定义一致。

射电天文学家也遵循这种惯例，这与國際天文聯會于1973年通过的决议一致。

从接收者的角度定义

在这种替代惯例中，偏振是从接收者的角度定义的。使用这种惯例时，左旋或右旋的确定方法是将左手或右手的拇指指向波源（即与波的传播方向相反），并将手指的卷曲方向与电场的时间旋转方向匹配。

与第一种惯例不同，这种惯例定义的波的旋向性与电场在空间中的螺旋性质一致。具体来说，如果将右旋波在时间上“冻结”，用右手手指卷曲围绕螺旋线时，拇指会指向螺旋线的推进方向。需要注意的是，在螺旋线的性质中，确定旋向性时拇指的指向方向并不重要。

当确定波是顺时针还是逆时针圆偏振时，同样从接收者的角度观察，面向波源并逆着波的传播方向，观察电场的时间旋转方向。

与第一种惯例一样，右旋对应于顺时针旋转，左旋对应于逆时针旋转。

许多光学教科书使用这种第二种惯例。國際光電工程學會和國際純化學和應用化學聯合會也采用这种惯例。

两种惯例的使用

如前所述，这两种惯例之间存在显著的混淆。一般来说，工程领域、量子物理学和射电天文学社区使用第一种惯例，即从波源的角度观察波。而在许多物理学教科书中，特别是涉及光学的内容，使用第二种惯例，即从接收者的角度观察光。

为避免混淆，在讨论偏振问题时，最好明确说明是“从波源的角度定义”还是“从接收者的角度定义”。

美国联邦标准1037C的档案中提出了两种矛盾的旋向性定义惯例。

需要注意的是，IEEE对右旋圆偏振（RHCP）和左旋圆偏振（LHCP）的定义与物理学家的定义相反。IEEE 1979天线标准将RHCP显示在庞加莱球的南极。IEEE使用右手定义RHCP，拇指指向发射方向，手指表示电场随时间旋转的方向。物理学家和工程师使用相反惯例的原因是：天文学观测通常是针对传入的波（朝向观察者），而大多数工程师则假设他们站在发射器后面，观察波远离他们传播。本文未使用IEEE 1979天线标准，也未使用IEEE工作中通常使用的+t惯例。

FM广播

犹他州湖山KENZ站的94.9 MHz、48 kW发射机的交叉偶极天线阵列。它辐射圆偏振无线电波。

调频广播电台有时采用圆偏振来改善信号对建筑物和车辆的穿透能力。这是国际电信联盟所称的“混合偏振”的一个例子，即无线电发射同时包含水平和垂直偏振分量。在美国，联邦通信委员会规定水平偏振是FM广播的标准，但也允许使用“圆偏振或椭圆偏振”。

二色性

圆二色性是指左旋和右旋圆偏振光在吸收上的差异。圆二色性是光谱学的一种形式，可用于确定分子的光学异构体和二级结构。

通常，任何光学活性分子在其吸收带中都会表现出这种现象。因此，大多数生物分子都会表现出圆二色性，因为它们含有右旋（如某些糖类）和左旋（如某些氨基酸）分子。值得注意的是，二級結構也会赋予其分子独特的圆二色性光谱特征。例如，蛋白质的α螺旋、β折叠和无规卷曲区域，以及核酸的双螺旋结构，都具有代表其结构的圆二色性光谱特征。

此外，在适当的条件下，即使是非手性分子也会表现出磁性圆二色，即由磁场诱导的圆二色性。

圆偏振发光

圆偏振发光（Circularly Polarized Luminescence, CPL）可以发生在发光体或发光体集合具有手性的情况下。发光的偏振程度通过不对称因子（dissymmetry factor）或各向异性因子（anisotropy factor）来量化，其公式为：

$g_{em}\ =\ 2\left({\theta _{\mathrm {left} }-\theta _{\mathrm {right} } \over \theta _{\mathrm {left} }+\theta _{\mathrm {right} }}\right)$

其中，$\theta _{\mathrm {left} }$和$\theta _{\mathrm {right} }$分别表示左旋和右旋圆偏振光的量子产率。g_em的最大绝对值为2，对应于纯左旋或右旋圆偏振光；最小绝对值为0，对应于线偏振或非偏振光。

数学描述

电场和磁场的电磁波方程的经典正弦平面波解为：

電磁波方程中電場和磁場的經典正弦平面波解为：

${\begin{aligned}\mathbf {E} (\mathbf {r} ,t)&=\left|\,\mathbf {E} \,\right|\mathrm {Re} \left\{\mathbf {Q} \left|\psi \right\rangle \exp \left[i\left(kz-\omega t\right)\right]\right\}\\\mathbf {B} (\mathbf {r} ,t)&={\dfrac {1}{c}}{\hat {\mathbf {z} }}\times \mathbf {E} (\mathbf {r} ,t)\end{aligned}}$

其中$k$是波數；

$\omega =ck$

是角频率，$\mathbf {Q} =\left[{\hat {\mathbf {x} }},{\hat {\mathbf {y} }}\right]$是一个正交的$2\times 2$矩阵，其列向量张成横向的x−y平面，$c$是光速。

电场振幅为$\left|\,\mathbf {E} \,\right|$，归一化的琼斯向量为：

$|\psi \rangle \ {\stackrel {\mathrm {def} }{=}}\ {\begin{pmatrix}\psi _{x}\\\psi _{y}\end{pmatrix}}={\begin{pmatrix}\cos \theta \exp \left(i\alpha _{x}\right)\\\sin \theta \exp \left(i\alpha _{y}\right)\end{pmatrix}}$

如果$\alpha _{y}$相对于$\alpha _{x}$旋转$\pi /2$弧度，且x和y方向的振幅相等，则波为圆偏振。此时琼斯向量为：

$|\psi \rangle ={1 \over {\sqrt {2}}}{\begin{pmatrix}1\\\pm i\end{pmatrix}}\exp \left(i\alpha _{x}\right)$

其中，加号表示左旋圆偏振，减号表示右旋圆偏振。在圆偏振的情况下，电场矢量的幅度恒定，并在x−y平面内旋转。如果基向量定义为：

$|\mathrm {R} \rangle \ {\stackrel {\mathrm {def} }{=}}\ {1 \over {\sqrt {2}}}{\begin{pmatrix}1\\-i\end{pmatrix}}$

和：

$|\mathrm {L} \rangle \ {\stackrel {\mathrm {def} }{=}}\ {1 \over {\sqrt {2}}}{\begin{pmatrix}1\\i\end{pmatrix}}$

则偏振态可以在“右旋-左旋基”（R-L基）中表示为：

$|\psi \rangle =\psi _{\mathrm {R} }|\mathrm {R} \rangle +\psi _{\mathrm {L} }|\mathrm {L} \rangle$

其中：

${\begin{aligned}\psi _{\mathrm {R} }~&{\stackrel {\mathrm {def} }{=}}~{\frac {1}{\sqrt {2}}}\left(\cos \theta +i\sin \theta \exp \left(i\delta \right)\right)\exp \left(i\alpha _{x}\right)\\\psi _{\mathrm {L} }~&{\stackrel {\mathrm {def} }{=}}~{\frac {1}{\sqrt {2}}}\left(\cos \theta -i\sin \theta \exp \left(i\delta \right)\right)\exp \left(i\alpha _{x}\right)\end{aligned}}$

和：

$\delta =\alpha _{y}-\alpha _{x}.$

天线

根据Balanis的研究，可以使用偶极子天线产生圆偏振（或接近圆偏振）的辐射：

“两个交叉的偶极子提供两个正交的场分量……如果两个偶极子完全相同，则它们在沿天顶方向上的场强度……将是相同的。此外，如果两个偶极子以90°的时间相位差（相位正交）馈电，则沿天顶方向的偏振将是圆偏振……实现两个正交场分量之间90°时间相位差的一种方法是通过将其中一个偶极子的传输线比另一个长或短四分之一波长。”第80页；

或螺旋型天線：

“为了实现圆偏振[在轴向或端模式下]……螺旋的周长C必须是……当C/波长≈1时接近最佳状态，且间距约为S = 波长/4，”第571页；

或贴片天线：

“……可以通过不同的馈电方式或对元件进行轻微的修改来获得圆偏振和椭圆偏振。若激励两个正交模式，并使它们之间存在90°的时域相位差，就可以获得圆偏振。这可以通过调整贴片的物理尺寸来实现。对于方形贴片元件，激励理想圆偏振的最简单方法是通过两个相邻边馈电。通过使用90°功率分配器馈电，可以获得四分之一波相位差，”第859页。

量子力学中

在量子力学中，光由光子组成。偏振是光自旋角动量的表现。具体来说，光子的自旋方向与圆偏振光的旋向性相关，光子束的自旋类似于电子束等粒子的自旋。

自然界中

金花金龟的外表面几乎只反射左旋圆偏振光。

自然界中已知只有少数几种机制能够系统地产生圆偏振光。1911年，阿尔伯特·迈克耳孙发现，从金色圣甲虫（Chrysina resplendens）反射的光是优先左偏振的。此后，圆偏振光在其他几种金龜子（如Chrysina gloriosa）以及一些甲壳类动物（如蝦蛄）中也被测量到。在这些情况下，底层机制是甲殼質表皮的分子级螺旋性。

螢火蟲幼体的生物发光也是圆偏振的，1980年有研究报道了光亮萤火虫（Photuris lucicrescens）和变色萤火虫（Photuris versicolor）种类的情况。对于萤火虫来说，找到微观的偏振机制较为困难，因为研究发现，幼虫的左右灯笼发出的偏振光方向相反。作者提出，光从对齐的光细胞内部的非均匀性开始时是线性偏振的，在通过线性双折射组织时便转变为圆偏振。

圆偏振光也已在从叶片和光合作用微生物反射的光中被检测到。

水-空气界面提供了另一个圆偏振光的来源。散射到表面并返回的阳光是线偏振的。如果这束光再经过全内反射回到下方，其垂直分量将发生相位变化。因此，对水下观察者来说，斯涅尔窗外的微弱光是（部分）圆偏振的。

自然界中较弱的圆偏振光来源包括线性偏振器的多重散射，例如恒星光的圆偏振，以及圆二色性介质的选择性吸收。

脉冲星的无线电辐射可以是强烈的圆偏振光。

报道称，两种蝦蛄能够探测到圆偏振光。

相关

• 偏振片
• 3D電影
• 手性
• 电磁波方程的正弦平面波解
• 星光偏振
• 波片