描述Prograde and retrograde circular orbital velocity.gif	Deutsch: Prograde und retrograde äquatoriale Kreisbahngeschwindigkeit um ein rotierendes schwarzes Loch. a ist der Spinparameter in Einheiten von J·c/G/M² mit J als dem Drehimpuls des schwarzen Lochs. Die x-Achse ist der Boyer-Lindquist-Radius r, und die y-Achse die lokale 3er-Geschwindigkeit v. Die linke vertikale Hilfslinie bezeichnet den Ereignishorizont (rH) bei r=(1+√(1-a²))GM/c², und die beiden an die Funktionskurven anschließenden vertikalen Hilfslinien die Radien für den pro- (r+) und retrograden (r-) Photonenkreis auf r±=2(1+cos(2arccos(±a))/3)GM/c². Weiterführende Erklärung: Herleitung / Details English: Prograde and retrograde equatorial circular orbit velocity around a rotating black hole. a is the spin parameter in units of J·c/G/M² where J ist the angular momentum of the black hole. The x-axis is the Boyer-Lindquist-Radius r, and the y-axis the local 3-velocity v. The left vertical gridline depicts the event horizon (rH) at r=(1+√(1-a²))GM/c², and the two vertical gridlines connecting to the function curves are the pro- (r+) and retrograde (r-) photon-orbits at r±=2(1+cos(2arccos(±a))/3)GM/c². Further reading: derivation / details
日期	2017年7月19日
來源	自己的作品
作者	Yukterez (Simon Tyran, Vienna)
其他版本

The pro- and retrograde circular orbital velocity is derived by setting

${\displaystyle {\rm {{\dot {p}}_{r}=v_{r}=v_{\theta }=0\ ,\ \ \theta =\pi /2\ ,\ \ v=v_{\phi }}}}$

and solving for ${\displaystyle {\rm {v_{\phi }}}}$. This gives the solution

${\displaystyle {\rm {v_{+}^{\circ }={\frac {a^{2}-2a{\sqrt {r}}+r^{2}}{{\sqrt {a^{2}+(r-2)r}}\left(a+r^{3/2}\right)}}}}}$

for the prograde and

${\displaystyle {\rm {v_{-}^{\circ }={\frac {a^{2}+2a{\sqrt {r}}+r^{2}}{{\sqrt {a^{2}+(r-2)r}}\left(a-r^{3/2}\right)}}}}}$

for the retrograde velocity.^[1] For photons with ${\displaystyle {\rm {v=1,\ \mu =0}}}$ one gets

${\displaystyle {\rm {r_{+}^{\circ }=2\left(\cos \left({\frac {2}{3}}\cos ^{-1}(-a)\right)+1\right)}}}$

for the prograde photon orbit radius (in Boyer-Lindquist-coordinates), and

${\displaystyle {\rm {r_{-}^{\circ }=2\left(\cos \left({\frac {2}{3}}\cos ^{-1}(+a)\right)+1\right)}}}$

for the retrograde one.^[2] In the Schwarzschild-limit with ${\displaystyle {\rm {a=0}}}$ both radii converge to ${\displaystyle {\rm {r^{\circ }=3}}}$.

Natural units: ${\displaystyle {\rm {G=M=c=1}}}$

Die pro- und retrograde Kreisbahngeschwindigkeit ergibt sich indem ${\displaystyle {\rm {{\dot {p}}_{r}=v_{r}=v_{\theta }=0\ ,\ \ \theta =\pi /2\ ,\ \ v=v_{\phi }}}}$

gesetzt und nach ${\displaystyle {\rm {v_{\phi }}}}$ aufgelöst wird. Damit ergibt sich als Lösung

${\displaystyle {\rm {v_{+}^{\circ }={\frac {a^{2}-2a{\sqrt {r}}+r^{2}}{{\sqrt {a^{2}+(r-2)r}}\left(a+r^{3/2}\right)}}}}}$

für die prograde und

${\displaystyle {\rm {v_{-}^{\circ }={\frac {a^{2}+2a{\sqrt {r}}+r^{2}}{{\sqrt {a^{2}+(r-2)r}}\left(a-r^{3/2}\right)}}}}}$

für die retrograde Kreisbahngeschwindigkeit.^[1] Für Photonen mit ${\displaystyle {\rm {v=1,\ \mu =0}}}$ ergibt sich daher

${\displaystyle {\rm {r_{+}^{\circ }=2\left(\cos \left({\frac {2}{3}}\cos ^{-1}(-a)\right)+1\right)}}}$

für den prograden Photonenkreisradius (in Boyer-Lindquist-Koordinaten), und

${\displaystyle {\rm {r_{-}^{\circ }=2\left(\cos \left({\frac {2}{3}}\cos ^{-1}(+a)\right)+1\right)}}}$

für den retrograden.^[2] Im Schwarzschild-Limit mit ${\displaystyle {\rm {a=0}}}$ fallen beide Radien auf ${\displaystyle {\rm {r^{\circ }=3}}}$.

Natürliche Einheiten: ${\displaystyle {\rm {G=M=c=1}}}$

(* Syntax: Mathematica *)
ClearAll["Global`*"]
vretro[a_,r_]:=(a^2+2 a Sqrt[r]+r^2)/(Sqrt[a^2+(-2+r) r] (a-r^(3/2))); 
vprogr[a_,r_]:=(a^2-2 a Sqrt[r]+r^2)/(Sqrt[a^2+(-2+r) r] (a+r^(3/2)));
rh = 1 + Sqrt[1 - a^2];
r1 = 2 (1 + Cos[2/3 ArcCos[-a]]);
r2 = 2 (1 + Cos[2/3 ArcCos[+a]]);
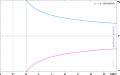
Do[Print[Rasterize[Grid[{{Show[
Plot[{vprogr[a, r], vretro[a, r]}, {r, 1, 10},
PlotRange->{{1, 10}, {-1, 1}},
GridLines->{{rh, r1, r2}, {}},
Frame->True, ImageSize->500, 
PlotStyle -> {{Blue, Thick}, {Magenta, Thick}}],
Graphics[{LightGray, Rectangle[{1, -1}, {rh, 1}]}]]}, 
{"a"->a}, {"rH"->rh}, {"r+"->r1}, {"r-"->r2}}, 
Alignment -> Left]]], 
{a, 0.0, 1.0, 0.1}]
(* kerr.yukterez.net *)

我，本作品的著作權持有者，決定用以下授權條款發佈本作品：

此檔案採用創用CC 姓名標示-相同方式分享 4.0 國際授權條款。

您可以自由：

• 分享 – 複製、發佈和傳播本作品
• 重新修改 – 創作演繹作品

惟需遵照下列條件：

• 姓名標示 – 您必須指名出正確的製作者，和提供授權條款的連結，以及表示是否有對內容上做出變更。您可以用任何合理的方式來行動，但不得以任何方式表明授權條款是對您許可或是由您所使用。
• 相同方式分享 – 若要根據本素材進行再混合、轉換或創作，則必須以與原作相同或相容的授權來發布您的作品。

https://creativecommons.org/licenses/by-sa/4.0CC BY-SA 4.0 Creative Commons Attribution-Share Alike 4.0 truetrue

1. ↑ ^{a b} Simon Tyran: Kreisbahnen in der Kerr-Raumzeit
2. ↑ ^{a b} Edward Teo: Spherical Photon Orbits Around A Kerr Black Hole

de.wikipedia.org/wiki/Kerr-Metrik