二分搜尋

此條目介紹的是查找有限有序数组中特定值位置的算法。关于计算连续函数中特定值位置的方法，请见「二分法 (數學)」。

二分搜尋
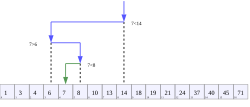二分查找过程示意，目标值为7
概况
類別	搜索算法
資料結構	数组
复杂度
平均時間複雜度	$O(\log n)$
最坏时间复杂度	$O(\log n)$
最优时间复杂度	$O(1)$
空間複雜度	$O(1)$
最佳解	是
相关变量的定义

「binary search」的各地常用譯名
中国大陸	二分查找、二分搜索
臺灣	二分搜尋

二分查找（英語：binary search）是用于查找有序数组中目标值位置的搜索算法。二分查找比较目标值与数组中间元素的大小，如果两者不相等，则会舍弃不可能包含目标值的那一半区间，然后在剩余区间重复此过程：每次选取新的中间元素并与目标值比较，直至找到目标或区间为空。若区间为空，则说明目标值不存在。

二分查找在最坏情况下的时间复杂度为对数级别，即需做$O(\log n)$次比较，其中$n$是数组元素的数量。除规模较小的数组外，二分查找通常比线性搜索更快。包括哈希表在内的某些数据结构，在搜索效率上可能超过二分查找，但二分查找还可用于查找最接近目标值的上界或下界，即使目标值不在数组中。

二分查找有许多其他形式。例如，分数级联能加快在多个数组中查找同一数值的速度，还能高效地解决计算几何等领域内的搜索问题；指数搜索则将搜索范围扩展至无界列表。二叉搜索树和B树等数据结构的实现也基于二分查找原理。

算法

二分查找适用于有序数组。其首先比较数组中间的元素与目标值：如果目标值与该元素匹配，则返回该元素在数组中的位置；如果目标值小于该元素，则在数组较小的那一半中继续查找；如果目标值大于该元素，则在数组较大的那一半中继续查找。通过这种方法，每次迭代都能将搜索范围缩小一半。

过程

给定一个包含$n$个元素的数组$A$，其中的值或记录分别为$A_{0},A_{1},A_{2},\ldots ,A_{n-1}$，且满足$A_{0}\leq A_{1}\leq A_{2}\leq \cdots \leq A_{n-1}$。假设目标值为$T$。下面的子程序使用二分查找来寻找$T$在数组$A$中的索引。

1. 令$L$为$0$，$R$为$n-1$。
2. 如果$L>R$，则搜索失败并终止。
3. 令$m$（中间元素的位置）为${\frac {L+R}{2}}$的向下取整值，即不大于${\frac {L+R}{2}}$的最大整数。
4. 如果$A_{m}<T$，则令$L$为$m+1$，回到步骤2。
5. 如果$A_{m}>T$，则令$R$为$m-1$，回到步骤2。
6. 如果$A_{m}=T$，则搜索完成，返回$m$。

这个迭代过程使用两个变量$L$和$R$来跟踪搜索边界。该过程可以用伪代码表示如下，其中变量名和类型与上文相同，floor为下取整函数，unsuccessful表示搜索失败时的特定返回值：

二分查找过程

function binary_search(A, n, T) is
    L := 0
    R := n − 1
    while L ≤ R do
        m := floor((L + R) / 2)
        if A[m] < T then
            L := m + 1
        else if A[m] > T then
            R := m − 1
        else:
            return m
    return unsuccessful

也可令$m$为${\frac {L+R}{2}}$的向上取整值。如此所做，若目标值在数组中出现多次，结果可能会有所不同。

替代过程

上述过程中，每次迭代都会检查中间元素（$m$）是否等于目标值（$T$）。而在其他一些实现中，仅剩下一个元素（即$L=R$）时，才会执行这项检查，这样每次迭代时就无需检查。这种方式的比较循环更快，因为每次迭代少了一次比较，但平均只需要多一次迭代。

赫尔曼·博滕布鲁赫于1962年首次发表了省略此检查的实现。

1. 令$L$为$0$，$R$为$n-1$。
2. 当$L\neq R$时，
   1. 令$m$（中间元素的位置）为${\frac {L+R}{2}}$的向上取整值，即不小于${\frac {L+R}{2}}$的最小整数。
   2. 如果$A_{m}>T$，令$R$为$m-1$。
   3. 否则说明$A_{m}\leq T$，令$L$为$m$。
3. 现在$L=R$，搜索完成。如果$A_{L}=T$，返回$L$。否则，搜索失败并终止。

该版本的伪代码如下，其中ceil是上取整函数：

function binary_search_alternative(A, n, T) is
    L := 0
    R := n − 1
    while L != R do
        m := ceil((L + R) / 2)
        if A[m] > T then
            R := m − 1
        else:
            L := m
    if A[L] = T then
        return L
    return unsuccessful

重复元素

若数组中有重复元素，算法会返回任一符合目标值的索引。例如，如果要搜索的数组为$[1,2,3,4,4,5,6,7]$，且目标值为$4$，那么算法返回第4个（索引为3）或第5个（索引为4）元素都是正确的。常规过程通常返回第4个元素（索引为3），但并不总是返回第一个重复项（例如数组$[1,2,4,4,4,5,6,7]$，这时依然返回第4个元素）。然而，有时需要找到目标值在数组中重复出现的最左侧或最右侧的元素。在上述例子中，第4个元素是值为4的最左侧元素，而第5个元素是值为4的最右侧元素。若对应元素存在，上述的替代过程总是会返回最右侧元素的索引。

查找最左侧元素的过程

要查找最左边的元素，可以使用以下过程：

1. 令$L$为$0$，$R$为$n$。
2. 当$L<R$时，
   1. 令$m$（中间元素的位置）为${\frac {L+R}{2}}$的向下取整值，即不大于${\frac {L+R}{2}}$的最大整数。
   2. 如果$A_{m}<T$，令$L$为$m+1$。
   3. 否则说明$A_{m}\geq T$，令$R$为$m$。
3. 返回$L$。

如果$L<n$且$A_{L}=T$，那么$A_{L}$是等于$T$的最左侧元素。即使$T$不在数组中，$L$也是$T$在数组中的排序位置，即数组中小于$T$的元素数量。

该版本的伪代码如下，其中floor是下取整函数：

function binary_search_leftmost(A, n, T):
    L := 0
    R := n
    while L < R:
        m := floor((L + R) / 2)
        if A[m] < T:
            L := m + 1
        else:
            R := m
    return L

查找最右侧元素的过程

要查找最右边的元素，可以使用以下过程：

1. 令$L$为$0$，$R$为$n$。
2. 当$L<R$时，
   1. 令$m$（中间元素的位置）为${\frac {L+R}{2}}$的向下取整值，即不大于${\frac {L+R}{2}}$的最大整数。
   2. 如果$A_{m}>T$，令$R$为$m$。
   3. 否则说明$A_{m}\leq T$，令$L$为$m+1$。
3. 返回$R-1$。

如果$R>0$ 且$A_{R-1}=T$，那么$A_{R-1}$是等于$T$的最右侧元素。即使$T$不在数组中，$n-R$也是数组中大于$T$的元素数量。

该版本的伪代码如下，其中floor是下取整函数：

function binary_search_rightmost(A, n, T):
    L := 0
    R := n
    while L < R:
        m := floor((L + R) / 2)
        if A[m] > T:
            R := m
        else:
            L := m + 1
    return R - 1

近似匹配

二分查找可计算近似匹配。上图中，目标值$5$本身不在数组中，但通过近似匹配，能计算出其排序位置、前驱、后继、最近邻

二分查找不仅能精确定位目标值，也可方便地扩展到近似匹配。例如，二分查找可以用来计算给定值的排序位置（即比它小的元素的数量）、前驱（前一个较小的元素）、后继（下一个较大的元素）、最近邻。范围查询（查找两个值之间的元素数量）可利用查询两次排序位置得到。

• 查询排序位置可以使用查找最左侧元素的过程来完成。程序的返回值即为小于目标值的元素数量。
• 查询前驱可以通过查询排序位置来执行。如果目标值的排序位置为$r$，那么其前驱的位置为$r-1$。
• 对于后继查询，可以查找最右侧元素。如果得到的结果为$r$，那么目标值的后继位置就是$r+1$。
• 目标值的最近邻是其前驱或后继之一，取决于哪个位置更接近。
• 区间查询也很简单。一旦知道了两个值的位置，区间内大于等于第一个值且小于第二个值的元素数量就是两个位置之差。考虑到是否需要将区间的端点包含在内，以及数组中是否包含与端点匹配的元素，其结果可能会增加或减少1。

性能

此章节中，${\textstyle \lfloor \cdot \rfloor }$表示向下取整，${\textstyle \log _{2}}$是以2为底的对数。

表示二分查找的树。这里要查找的数组是$[20,30,40,50,80,90,100]$，目标值是$40$

最坏情况下，搜索到达树的最深层；而最好情况是目标值恰为中间元素

二分查找的过程可以构建成一棵二叉树，从而得到其比较次数并分析性能。树的根节点是数组的中间元素，左半部分的中间元素是根节点的左子节点，右半部分的中间元素是根节点的右子节点，其余部分以类似方式构建。搜索过程从根节点开始，根据目标值是小于还是大于当前节点的值来选择遍历左子树还是右子树。

最坏情况下，二分查找需要比较${\textstyle \lfloor \log _{2}(n)+1\rfloor }$次，此时搜索会达到树的最深层。对于任何二分查找，树的层数总为${\textstyle \lfloor \log _{2}(n)+1\rfloor }$。若目标元素不在数组中，可能会发生最坏情况：若${\textstyle n}$可以表示为2的某次幂减1，那么查找过程总会遍历到最深层，一定会发生最坏情况；否则，搜索过程可能会在倒数第二层中止，此时比较了${\textstyle \lfloor \log _{2}(n)\rfloor }$次，比最坏情况少一次。

平均情况下，当目标元素在数组中时，二分查找的比较次数是$\lfloor \log _{2}(n)\rfloor +1-(2^{\lfloor \log _{2}(n)\rfloor +1}-\lfloor \log _{2}(n)\rfloor -2)/n$（假设每个元素被搜索的概率相等），近似于$\log _{2}(n)-1$；若目标元素不在数组中，二分查找的比较次数平均为$\lfloor \log _{2}(n)\rfloor +2-2^{\lfloor \log _{2}(n)\rfloor +1}/(n+1)$（假设范围内及范围外的元素被搜索的概率相等）。

最好情况下，即目标值正好是数组的中间元素，二分查找在一次比较后就能返回其位置。

从迭代次数的角度看，没有任何一种仅通过比较元素大小进行搜索的算法，在平均情况和最坏情况下的性能优于二分查找。表示二分查找的比较树除最底层外，每一层都是完全填满的，因此层数最少。如果不以此方式构造树，搜索算法在每次迭代中只能排除较少的元素，从而增加平均情况和最坏情况下所需的迭代次数。其他基于元素比较的搜索算法便属于这种情况：虽然它们在某些目标值上可能更快，但综合考虑所有元素时，其平均性能都不及二分查找。二分查找通过每次将数组一分为二，保证两个子数组的大小尽可能相近。

空间复杂度

二分查找需要使用三个指针（可能为数组的索引，或指向内存地址的指针），与数组本身的大小无关。因此，在word RAM计算模型中，二分查找的空间复杂度为$O(1)$。

平均情况的推导

二分查找的平均迭代次数取决于每个元素被搜索的概率，而成功搜索与失败搜索的平均情况是不同的。对于成功搜索，则需假设每个元素被搜索的概率相等；对于失败搜索，则需假设数组元素之间及元素之外的每个区间被搜索的概率相等。成功搜索的平均情况是搜索数组中每个元素所需迭代次数之和除以元素数量$n$；失败搜索的平均情况则是搜索数组各区间所需迭代次数之和除以区间数量$n+1$。

成功搜索

在二叉树的表示法中，一次成功搜索可以表示为从树的根节点到目标节点的路径，称为「内部路径」（internal path）。路径长度等于路径中经过的边（节点之间的连接）数目。如果一条路径长度为$l$，则对应搜索所需的迭代次数为$l+1$（包括初始迭代）。所有内部路径长度之和称作「内部路径长度」（internal path length）。由于从根节点到任何特定节点仅存在一条路径，因此每条内部路径表示对特定元素的一次搜索。如果有$n$个元素（$n$为正整数），内部路径长度记为$I(n)$，则成功搜索的平均迭代次数$T(n)=1+{\frac {I(n)}{n}}$（其中$1$表示初始迭代）。

由于二分查找是基于元素比较的最优搜索算法，因此问题可简化为求解含$n$个节点的所有可能二叉树中的最小内部路径长度，表达式如下：

$I(n)=\sum _{k=1}^{n}\left\lfloor \log _{2}(k)\right\rfloor$

例如，对于含7个元素的数组，根节点对应的搜索需1次迭代，下一层的两个节点各需2次，再下一层的四个节点各需3次。因此，此时内部路径长度为：

$\sum _{k=1}^{7}\left\lfloor \log _{2}(k)\right\rfloor =0+2(1)+4(2)=2+8=10$

根据成功搜索平均情况的公式，此时的平均迭代次数为$1+{\frac {10}{7}}=2{\frac {3}{7}}$。

上述内部路径长度$I(n)$的求和公式可进一步化简为：

$I(n)=\sum _{k=1}^{n}\left\lfloor \log _{2}(k)\right\rfloor =(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2$

将此式代入成功搜索平均迭代次数$T(n)$的表达式中，得到：

$T(n)=1+{\frac {(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2}{n}}=\lfloor \log _{2}(n)\rfloor +1-(2^{\lfloor \log _{2}(n)\rfloor +1}-\lfloor \log _{2}(n)\rfloor -2)/n$

当$n$为整数时，其与前述成功搜索的平均情况公式完全相同。

失败搜索

失败搜索可用在树中增加额外节点的方式表示，这种结构称为扩展二叉树（extended binary tree）。当树中已有节点（即内部节点）不足两个子节点时，页需为其添加额外的子节点（即外部节点），使每个内部节点都有两个子节点。这样一来，失败的搜索过程便可表示为从根节点到外部节点的一条路径，这个外部节点的父节点即为搜索结束时剩下的唯一元素。从根节点到外部节点的路径称为「外部路径」（external path）。所有外部路径的长度之和称作「外部路径长度」（external path length）。若元素个数为正整数$n$，外部路径长度为$E(n)$，则失败搜索的平均迭代次数$T'(n)={\frac {E(n)}{n+1}}$（其中$1$表示初始迭代）。公式中除以$n+1$而非$n$的原因是，树中有$n+1$条外部路径，它们分别表示数组元素之间以及数组边界之外的各个区间。

同样地，这一问题可以简化为确定含$n$个节点的所有二叉树中的最小外部路径长度。对于任意二叉树，外部路径长度与内部路径长度之间满足$E(n)=I(n)+2n$。将先前得到的$I(n)$表达式代入，则有：

$E(n)=I(n)+2n=\left[(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2\right]+2n=(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}$

再将上式代入平均迭代次数$T'(n)$的公式，便可求出失败搜索的平均迭代次数：

$T'(n)={\frac {(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}}{(n+1)}}=\lfloor \log _{2}(n)\rfloor +2-2^{\lfloor \log _{2}(n)\rfloor +1}/(n+1)$

另一过程的性能

前文定义的二分查找过程，每次迭代需要做一次或两次比较，其中每次迭代都会检查中间元素是否与目标相等。假设每个元素被搜索到的概率均等，那么平均每次迭代的比较次数为1.5次。算法的一种实现方法是在搜索结束后检查中间元素是否与目标值相等。平均而言，这种方法每次迭代可减少0.5次比较，略微降低了大部分计算机上每次迭代的运行时间。然而，这种方式一定会达到最多的迭代次数，平均而言搜索过程会额外增加一次迭代。因为即使在最坏情况下，二分查找的比较循环也只执行${\textstyle \lfloor \log _{2}(n)+1\rfloor }$次，因此除非${\textstyle n}$极大，否则每次迭代效率的微小提升不足以弥补增加的额外迭代次数。

运行时间和缓存使用

在分析二分查找的性能时，另一个需要考虑的因素是比较两个元素所需的时间。整数和字符串的比较时间通常与其编码长度（一般以位数表示）呈线性关系。例如，与32位无符号整数相比，比较两个64位无符号整数的时间最多是前者的两倍，最坏情况出现在整数完全相同时。若元素的编码长度较大（例如大整数类型或长字符串），比较操作的开销则会显著增加。此外，比较浮点数（实数在计算机中最常用的表示方式）通常也比整数和短字符串耗时更多。

多数计算机架构中，CPU内部配有独立于内存（RAM）的硬件缓存，容量较小但速度极快。因此，考虑到访问局部性，多数CPU会存储最近访问的内存地址及其附近地址的数据。就数组而言，CPU访问某个元素时，会同时缓存该元素以及在RAM中与之相邻的元素，从而更快地顺序访问索引相近的数组元素。然而，二分查找每次跳跃到数组中点，往往跨越多个缓存行，不像线性搜索或哈希表的线性探测那样具有良好局部性。因此在较大数组上，实际耗时可能略高于理论预期。

二分搜索与其他方案

在有序数组中，当插入和删除操作与查找操作交替进行时，使用二分查找的效率会非常低下。每次插入或删除操作的时间复杂度为${\textstyle O(n)}$。此外，有序数组的内存使用可能较为复杂，特别是在需要频繁插入元素的情况下。其他一些数据结构能更高效地支持插入与删除操作。二分查找可以用于精确匹配和集合成员检测（即判断目标值是否存在于某个集合内）。虽然一些数据结构能够更快地精确匹配与检测集合成员，但二分查找还可用于高效地执行近似匹配，通常不论值的类型或结构如何，其近似匹配的性能都能达到${\textstyle O(\log n)}$。此外，有序数组上还能高效完成一些操作，例如获取最小值和最大值。

线性搜索

线性搜索是简单的搜索算法，其逐个检查记录，直到找到目标值为止。线性搜索可以在链表上实现，其插入和删除操作比数组更快。对于有序数组，除非数组很短，否则二分查找通常比线性搜索更快。不过二分查找需要提前对数组排序，所有基于元素比较的排序算法（例如快速排序和归并排序），最坏情况下都至少需要做${\textstyle O(n\log n)}$次比较。与线性搜索不同，二分查找还能高效地进行近似匹配。此外，在有序数组中，查找最大或最小元素等操作可以高效完成，而无序数组则无法做到。

二叉树

二叉搜索树的搜索算法类似于二分查找

二叉搜索树是基于二分查找原理构建的二叉树数据结构。树中元素按序排列，每个元素都可使用类似二分查找的方法执行搜索，其平均时间复杂度为对数级别。二叉搜索树的插入和删除操作平均也为对数时间，通常比有序数组插入和删除的线性时间更快。同时，二叉树也保留了有序数组的所有操作能力，包括范围查询和近似查询。

不过，二分查找在搜索操作上通常更高效，因为二叉搜索树往往不是完美平衡的，性能会稍逊于二分查找。即使是平衡树（能够自我平衡的二叉搜索树），也很少能达到理论上层数最少的状态。非平衡二叉树甚至可能严重失衡，内部节点（具有两个子节点的节点）数量很少，此时的平均和最坏搜索性能可能接近${\textstyle n}$次比较。此外，二叉搜索树占用的空间也比有序数组更大。

二叉搜索树在外部存储设备（如硬盘）的搜索中具有优势，因为可以在文件系统中有效组织。B树推广了这一树结构的组织方式，经常用于数据库和文件系统等长期存储系统。

哈希表

哈希表是将键映射到对应记录的数据结构，一般使用哈希函数实现。对于关联数组，哈希表通常比有序数组上的二分查找更快。大部分哈希表的实现，其平均时间复杂度仅为平摊的常数时间。但哈希表只在搜索失败时告知目标不存在，而不能给出邻近值的信息，因此不适合近似匹配，包括查找下一个较小值、下一个较大值或者最近的键值等操作。二分查找则非常适合近似匹配，且能在对数时间内完成。此外，诸如查找最大或最小元素的操作在有序数组上可高效完成，而哈希表无法做到。

集合

集合成员检测是与搜索类似的问题，任何像二分查找这样的查找算法都可用于集合成员检测。但也有一些专门用于集合成员检测的算法。例如，当键值范围有限时，位数组是最简单的选择。位数组紧凑地存储一系列位，每位代表一个特定范围内的键值。位数组的速度非常快，查询仅需${\textstyle O(1)}$时间。朱迪矩阵中的Judy1类型则能有效处理64位键值。

对于近似结果，布隆过滤器是基于哈希函数的概率型数据结构，其使用位数组和多个哈希函数对键编码，以存储键集合。多数情况下，布隆过滤器比位数组的空间利用率更高，且速度也不会明显变慢：若使用${\textstyle k}$个哈希函数，成员查询仅需${\textstyle O(k)}$时间。不过，布隆过滤器存在误报问题。

其他数据结构

在某些情况下，一些数据结构可能在搜索操作和其他适用于有序数组的操作上比二分查找更高效。对于搜索、近似匹配及有序数组上的一些操作，可以使用专门的数据结构，如van Emde Boas树、融合树、字典树（trie）、位数组。这些数据结构可能比二分查找更加高效，但通常只有在特定属性的键值（如小整数键值）上更快，否则可能会导致时间或空间效率降低。只要键值能被排序，前述操作在有序数组上仍能保持较高的效率。某些数据结构（如朱迪矩阵）结合了多种方法，不仅缓解了这些问题，还能保持较高效率，同时能够近似匹配。

其他形式

统一二分查找

主条目：统一二分查找

统一二分查找存储当前中间元素到下一次迭代的中间元素间的索引差值

统一二分查找存储的不是上下界，而是从当前中间元素到下一次迭代的中间元素间的索引差值，会将之事先存入查找表中。例如，要搜索的数组若为[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]，当前的中间元素$m$是6。此时，左侧子数组[1, 2, 3, 4, 5]的中间元素是3，右侧子数组[7, 8, 9, 10, 11]的中间元素是9。统一二分查找会存储3这个差值（因为从6到左右两个中间元素的索引距离都是3）。为了缩小搜索空间，算法每次将这个差值与当前中间索引相加减。在某些不便于计算中点的系统（如十进制计算机）中，这种方法可能更快。

指数搜索

主条目：指数搜索

指数搜索的可视化图，展示了如何确定后续二分查找的上限

指数搜索将二分查找扩展到无界列表。它首先查找第一个索引为2的幂且元素大于目标值的位置，然后将该位置作为上界，再切换至二分查找。若目标值的位置为${\textstyle x}$，则在开始二分查找之前，指数搜索最多需要进行${\textstyle \lfloor \log _{2}x+1\rfloor }$次迭代，此后最多再进行${\textstyle \lfloor \log _{2}x\rfloor }$次二分查找的迭代。指数搜索也适用于有界列表，但仅当目标值位于数组的开头附近时才比直接使用二分查找更高效。

插值搜索

主条目：插值搜索

插值搜索使用线性插值进行查找的可视化图。在此例中，由于对目标值在数组中位置的估计非常准确，因此无需进一步查找。其他实现可能会使用不同的函数来估计目标位置

插值搜索不是每次计算中点，而是估算目标元素的位置。估算过程考虑数组的最小值、最大值以及数组长度。其基本思路是：中点在很多情况下并非最理想的猜测位置。例如，如果目标值接近数组中的最大值，那么目标值很可能靠近数组末尾。

插值函数中最常见的是线性插值。设数组为$A$，下界为$L$，上界为$R$，目标值为$T$，则目标位置的估计值为$(T-A_{L})/(A_{R}-A_{L})$。若使用线性插值，且数组元素分布均匀或接近均匀，则插值搜索的比较次数为${\textstyle O(\log \log n)}$。

实际上，对于较小的数组，插值搜索由于有额外的计算开销，其速度通常比二分查找慢。尽管插值搜索的时间复杂度增长更慢，但只有在数组规模较大时，这种优势才能抵消额外计算所需的开销。

分数级联

主条目：分数级联

分数级联的原理图，展示了每个数组如何拥有指向其他数组中特定元素（例如每隔一个元素）的指针，从而只需执行一次二分查找即可查找所有关联数组

分数级联是用于在多个有序数组中快速搜索同一元素的技术。如果逐个搜索每个数组，时间复杂度为${\textstyle O(k\log n)}$，其中${\textstyle k}$为数组个数。分数级联在每个数组中存储关于元素在其他数组位置的信息，将时间复杂度降至${\textstyle O(k+\log n)}$。

分数级联最初是为了解决计算几何中的多种搜索问题而开发的。后来，它也被应用于数据挖掘和互联网协议（IP）路由中。

图的推广形式

二分查找还被推广到某些类型的图结构，其中目标值存储于图的顶点中，而非数组元素内。二叉搜索树即是这种推广的特例。当在树中查询某个节点时，算法要么确定这个节点就是目标，要么知道目标元素所在的子树位置。但推广形式还可以更进一步：给定无向正权图及目标顶点，每次查询一个顶点时，算法要么知道这个顶点就是目标，要么获得从该顶点到目标顶点的最短路径上的某条边信息。标准二分查找实际上是图为路径时的特例，而二叉搜索树则对应于当查询的顶点不为目标时给出左或右子树边的情况。对于所有无向正权图，均存在算法可在最坏情况下以$O(\log n)$次查询找到目标顶点。

噪声二分查找

噪声二分查找过程中，每对元素的比较都有一定概率出错

噪声二分查找用于处理算法无法可靠地比较数组元素的情况，即比较每对元素大小时，都有一定概率出错。噪声二分查找可在给定的概率下确定目标元素正确的位置，这一概率控制着结果的可靠性。任何噪声二分查找过程期望比较次数至少为$(1-\tau ){\frac {\log _{2}(n)}{H(p)}}-{\frac {10}{H(p)}}$，其中$H(p)=-p\log _{2}(p)-(1-p)\log _{2}(1-p)$ 为二元熵函数，$\tau$表示过程给出错误位置的概率。噪声二分查找问题也可视作Rényi-Ulam game的特例，即20个问题的回答可能出错之变体。

量子二分查找

经典计算机执行二分查找时，在最坏情况下的迭代次数严格为${\textstyle \lfloor \log _{2}n+1\rfloor }$。量子算法执行二分查找的查询次数（对应经典算法的迭代次数）仍然与${\textstyle \log _{2}n}$成正比，但常数因子小于1，因此在量子计算机上具有更低的时间复杂度。任何精确的量子二分查找算法（即总能返回正确结果的算法），最坏情况下至少需要${\textstyle {\frac {1}{\pi }}(\ln n-1)\approx 0.22\log _{2}n}$次查询（其中${\textstyle \ln }$为自然对数）。目前已经存在一种精确的量子二分查找算法，其在最坏情况下的查询次数为${\textstyle 4\log _{605}n\approx 0.433\log _{2}n}$。相比之下，格罗弗算法是用于搜索无序列表的最优量子算法，其所需的查询次数为$O({\sqrt {n}})$。

历史

排序列表元素以提高查找效率，这一思想古人亦有之。目前已知最早的实例是约公元前200年巴比伦的「Inakibit-Anu」泥板，其包含约500个六十进制的数字及其倒数，数字按字典序排列，以便更快地找到特定的元素。此外，爱琴海诸岛上也发现了一些按照姓名首字母排序的人名列表。1286年完成的拉丁语词典《Catholicon》，首次给出了完整的字母排序规则，而不仅仅是依照单词前几个字母排序。

1946年，约翰·莫奇利在摩尔学院讲座（一门计算机科学领域的奠基性课程）中首次提及了二分查找。1957年，威廉·韦斯利·彼得森发表了首个插值搜索算法。早期的二分查找算法均只能用于长度为2的幂次减一的数组。直至1960年，德里克·亨利·莱默提出适用于任意长度数组的二分查找算法。1962年，赫尔曼·博滕布鲁赫在ALGOL 60语言中实现了另一种二分查找版本，将判断相等的比较操作放在末尾，虽使平均迭代次数增加了一次，但每次迭代所需的比较次数减少至一次。统一二分查找则由斯坦福大学的A.K.钱德拉（A. K. Chandra）于1971年开发。1986年，贝尔纳·沙泽勒与利奥尼达斯·J·吉巴斯引入了「分数级联」概念，用以解决计算几何中的诸多查找问题。

实现问题

尽管二分查找的基本思想相对简单，但其细节却出奇复杂。

——高德纳

乔恩·本特利在为职业程序员开设的一门课程中布置了二分查找的练习，发现90%的学生在数小时后仍未能给出正确的解答。主要原因是算法实现有误而无法运行，或是在极少数边界情况下返回错误答案。1988年发表的一项研究显示，二十本教材中只有五本给出了准确的二分查找代码。此外，本特利自身在1986年出版的《编程珠玑》一书中给出的二分查找实现存在溢出错误，这个错误在二十多年里未被发现。Java编程语言库中的二分查找实现也存在相同的溢出问题，且该问题持续了九年多。

在实际编程中，表示索引的变量通常是固定大小的整数。因此在处理非常大的数组时，可能会导致算术溢出。如果使用${\frac {L+R}{2}}$计算中点，即使$L$和$R$的值都在所用数据类型的表示范围内，$L+R$的值仍可能会超过范围。如果$L$和$R$都是非负数，可以通过计算$L+{\frac {R-L}{2}}$来避免这种情况。

如果循环的退出条件定义不正确，可能会导致无限循环。当$L$超过$R$时，表示搜索失败，必须返回失败的信息。另外，循环应在找到目标元素时退出；若不这么做，那么在循环结束后，必须检查是否成功找到目标元素。本特利发现，大多数在实现二分查找时出错的程序员，都是在定义退出条件时犯了错。

库支持

许多编程语言的标准库包含二分查找例程：

• C语言在其标准库中提供了bsearch()函数，通常使用二分查找实现，尽管官方标准中并未强制要求。
• C++的标准库中提供了binary_search()、lower_bound()、upper_bound()、equal_range()函数。
• D语言的标准库Phobos在std.range模块中提供了SortedRange类型（由sort()和assumeSorted()函数返回），该类型包含contains()、equaleRange()、lowerBound()、trisect()方法，这些方法默认对提供随机访问的范围使用二分查找技术。
• COBOL提供了SEARCH ALL动词，用于对COBOL有序表执行二分查找。
• Go的sort标准库包包含Search、SearchInts、SearchFloat64s、SearchStrings函数，分别实现了通用的二分查找，以及针对整数、浮点数、字符串切片的特定实现。
• Java在标准java.util包的Arrays和Collections类中提供了一组重载的binarySearch()静态方法，用于对Java数组和List（列表）执行二分查找。
• Microsoft的.NET Framework 2.0在其集合基类中提供了二分查找算法的静态泛型版本，例如System.Array的BinarySearch<T>(T[] array, T value)方法。
• 对于Objective-C，Cocoa框架在Mac OS X 10.6及以上版本中提供了NSArray -indexOfObject:inSortedRange:options:usingComparator:方法；苹果的Core Foundation C框架也包含CFArrayBSearchValues()函数。
• Python提供了模块bisect，在插入元素后仍能保持列表的有序状态，而无需每次插入元素后都对列表排序。
• Ruby的Array类包含带有内置近似匹配的bsearch方法。
• Rust的切片原始类型提供了binary_search()、binary_search_by()、binary_search_by_key()、partition_point()方法。

参见

• 乘性二分查找

注释和参考文献

来源

• Bentley, Jon. Programming pearls 2nd. Addison-Wesley. 2000. ISBN 978-0-201-65788-3 （英语）. 
• Butterfield, Andrew; Ngondi, Gerard E. A dictionary of computer science 7th. Oxford, UK: Oxford University Press. 2016. ISBN 978-0-19-968897-5 （英语）. 
• Chang, Shi-Kuo. Data structures and algorithms. Software Engineering and Knowledge Engineering 13. Singapore: World Scientific. 2003. ISBN 978-981-238-348-8 （英语）. 
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford. Introduction to algorithms 3rd. MIT Press and McGraw-Hill. 2009. ISBN 978-0-262-03384-8 （英语）. 
• Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford. 算法导论. 由殷建平; 徐云; 王刚; 刘晓光; 苏明; 邹恒明; 王宏志翻译 第3版. 北京: 机械工业出版社. 2013. ISBN 978-7-111-40701-0 （中文（中国大陆））. 
• Fitzgerald, Michael. Ruby pocket reference. Sebastopol, California: O'Reilly Media. 2015. ISBN 978-1-4919-2601-7 （英语）. 
• Goldman, Sally A.; Goldman, Kenneth J. A practical guide to data structures and algorithms using Java. Boca Raton, Florida: CRC Press. 2008. ISBN 978-1-58488-455-2 （英语）. 
• Kasahara, Masahiro; Morishita, Shinichi. Large-scale genome sequence processing. London, UK: Imperial College Press. 2006. ISBN 978-1-86094-635-6 （英语）. 
• Knuth, Donald. Fundamental algorithms. The Art of Computer Programming 1 3rd. Reading, MA: Addison-Wesley Professional. 1997. ISBN 978-0-201-89683-1 （英语）. 
• Knuth, Donald. Sorting and searching. The Art of Computer Programming 3 2nd. Reading, MA: Addison-Wesley Professional. 1998. ISBN 978-0-201-89685-5 （英语）. 
• Knuth, Donald. Combinatorial algorithms. The Art of Computer Programming 4A 1st. Reading, MA: Addison-Wesley Professional. 2011. ISBN 978-0-201-03804-0 （英语）. 
• Moffat, Alistair; Turpin, Andrew. Compression and coding algorithms. Hamburg, Germany: Kluwer Academic Publishers. 2002. ISBN 978-0-7923-7668-2. doi:10.1007/978-1-4615-0935-6 （英语）. 
• Sedgewick, Robert; Wayne, Kevin. Algorithms 4th. Upper Saddle River, New Jersey: Addison-Wesley Professional. 2011. ISBN 978-0-321-57351-3 （英语）.  Condensed web version ; book version .
• Sedgewick, Robert; Wayne, Kevin. 算法. 由谢路云翻译 第4版. 北京: 人民邮电出版社. 2012. ISBN 978-7-115-29380-0 （中文（中国大陆））. 
• Stroustrup, Bjarne. The C++ programming language 4th. Upper Saddle River, New Jersey: Addison-Wesley Professional. 2013. ISBN 978-0-321-56384-2 （英语）. 

外部链接

• Anthony Lin. Binary search algorithm (PDF). 理學維基期刊. 2019-07-02, 2 (1): 5. ISSN 2470-6345. doi:10.15347/WJS/2019.005. Wikidata Q81434400 （英语）. 。该论文内容取自英语维基百科的对应条目，于2018年经过外部学术同行评审。
• NIST Dictionary of Algorithms and Data Structures: binary search
• Comparisons and benchmarks of a variety of binary search implementations in C （互联网档案馆的存檔，存档日期2019-09-25.）